题目内容
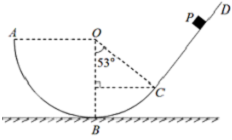
如图所示,半径为R的光滑圆弧轨道ABC竖直放置,A与圆心O等高,B为轨道的最低点,该圆弧轨道与一粗糙直轨道CD相切于C,OC与OB的夹角为53°。一质量为m的小滑块从P点静止开始下滑,PC间距离为R,滑块在CD上所受滑动摩擦力为重力的0.3倍。(sin53°,cos53°=0.6)求:
(1)滑块从P点滑到B点的过程中,重力势能减少多少?
(2)滑块第一次经过B点时对轨道的压力大小;
(3)为保证滑块不从A处滑出,PC之间的最大距离是多少?

(1)滑块从P点滑到B点的过程中,重力势能减少多少?
(2)滑块第一次经过B点时对轨道的压力大小;
(3)为保证滑块不从A处滑出,PC之间的最大距离是多少?
(1)1.2mgR;(2)2.8mg;(3)1.2R
试题分析:(1)设PC间的垂直高度为h
由几何关系得h1=Rsin53°=0.8R,CB间的竖直高度h2=R-Rcos53°=0.4R
∴PB间高度差h=h1+h2=1.2R,所以滑块从P滑到B减少的重力势能为△Ep=mgh=1.2mgR;
(2)对B点,由牛顿第二定律知
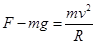
从P到B,由动能定理:
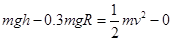
联立解得 F=2.8mg;
设PC之间的最大距离为L时,滑块第一次到达A时速度为零,则对整个过程应用动能定理
mgLsin53°+mgR(1-cos53°)-mgR-0.3mgL=0
代入数值解得 L=1.2R

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
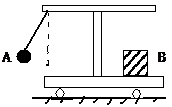
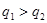 。当-q1、-q2经过P点时速度大小分别为v1、v2,加速度大小分别为a1、a2,下列关系式正确的是
。当-q1、-q2经过P点时速度大小分别为v1、v2,加速度大小分别为a1、a2,下列关系式正确的是 
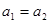
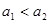

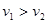

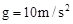 ,结果保留2位有效数字)。
,结果保留2位有效数字)。