题目内容
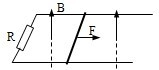 (2004?淮安二模)如图所示,一对平行光滑轨道放置大水平面上,两轨道相距L=1m,两轨道之间用电阻R=2Ω连接,有一质量为m=0.5kg的导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向下.现用水平拉力沿轨道方向拉导体杆,使导体杆从静止开始做匀加速运动.经过位移s=0.5m后,撤去拉力,导体杆又滑行了相同的位移s后停下.
(2004?淮安二模)如图所示,一对平行光滑轨道放置大水平面上,两轨道相距L=1m,两轨道之间用电阻R=2Ω连接,有一质量为m=0.5kg的导体杆静止地放在轨道上,与两轨道垂直,杆及轨道的电阻皆可忽略不计,整个装置处于磁感应强度B=2T的匀强磁场中,磁场方向垂直轨道平面向下.现用水平拉力沿轨道方向拉导体杆,使导体杆从静止开始做匀加速运动.经过位移s=0.5m后,撤去拉力,导体杆又滑行了相同的位移s后停下.求:(1)全过程中通过电阻R的电荷量.
(2)拉力的冲量.
(3)匀加速运动的加速度.
(4)画出拉力随时间变化的F-t图象.
分析:(1)根据电量表达式、闭合电路欧姆定律、法拉第电磁感应定律,即可求解;
(2)根据动量定理,可求出拉力的冲量;
(3)根据牛顿第二定律,结合安培力公式与运动学公式,即可求解;
(4)由牛顿第二定律,与安培力公式可求出拉力与时间的关系式,并作出图象.
(2)根据动量定理,可求出拉力的冲量;
(3)根据牛顿第二定律,结合安培力公式与运动学公式,即可求解;
(4)由牛顿第二定律,与安培力公式可求出拉力与时间的关系式,并作出图象.
解答:解:
(1)设全过程中平均感应电动势为E,平均感应电流为I,时间△t,
则通过电阻R的电荷量:
q=I△t,I=
,E=
=
.
得q=
=1C
(2、3)拉力撤去时,导体杆的速度为v,拉力撤去后杆运动时间为△t2,平均感应电流为I2,
根据牛顿第二定律有:
BI2L=m
,
即有,BI2L△t2=mv
∵I2△t2=q′=
=
∴
=mv,
v=
=
m/s=2m/s
所以a=
=4m/s2
 根据动量定理,则有
根据动量定理,则有
拉力的冲量I=mv=0.5×2N?s=1N?s
(4)F=ma+BIL=ma+B2L2
,
拉力作用时间t=
=0.5s,此时Fmax=6N;
t=0时,F=ma=2N
画出拉力随时间变化的F-t图象
答:(1)全过程中通过电阻R的电荷量为1C,
(2)拉力的冲量1N?s
(3)匀加速运动的加速度为4m/s2.
(4)图象如右图所示.
(1)设全过程中平均感应电动势为E,平均感应电流为I,时间△t,
则通过电阻R的电荷量:
q=I△t,I=
| E |
| R |
| △? |
| △t |
| 2BLs |
| △t |
得q=
| 2BLs |
| R |
(2、3)拉力撤去时,导体杆的速度为v,拉力撤去后杆运动时间为△t2,平均感应电流为I2,
根据牛顿第二定律有:
BI2L=m
| v |
| △t2 |
即有,BI2L△t2=mv
∵I2△t2=q′=
| q |
| 2 |
| BLs |
| R |
∴
| B2L2s |
| R |
v=
| B2L2s |
| mR |
| 22×12×0.5 |
| 0.5×2 |
所以a=
| v2 |
| 2s |
 根据动量定理,则有
根据动量定理,则有拉力的冲量I=mv=0.5×2N?s=1N?s
(4)F=ma+BIL=ma+B2L2
| at |
| R |
拉力作用时间t=
| v |
| a |
t=0时,F=ma=2N
画出拉力随时间变化的F-t图象
答:(1)全过程中通过电阻R的电荷量为1C,
(2)拉力的冲量1N?s
(3)匀加速运动的加速度为4m/s2.
(4)图象如右图所示.
点评:考查电学知识,并与力、运动相综合,掌握法拉第电磁感应定律、闭合电路欧姆定律、牛顿第二定律等规律的应用,同时学会作关系式的图象.

练习册系列答案
相关题目
 (2004?淮安二模)如图所示,带有活塞的气缸中封闭一定质量的理想气体,将一个半导体NTC热敏电阻R置于气缺中,热敏电阻与容器外的电源E和电流表 组成闭合回路,气缸和活塞具有良好的绝热(与外界无热交换)性能.若发现电流表的读数增大时,以下判断正确的是( )
(2004?淮安二模)如图所示,带有活塞的气缸中封闭一定质量的理想气体,将一个半导体NTC热敏电阻R置于气缺中,热敏电阻与容器外的电源E和电流表 组成闭合回路,气缸和活塞具有良好的绝热(与外界无热交换)性能.若发现电流表的读数增大时,以下判断正确的是( )
 (2004?淮安二模)卡车在行驶时,货物随车厢底板上下振动而不脱离底板,设货物作简谐运动.以竖直向上为正方向,其振动图象如图所示,则在图象上a、b、c、d四点中货物对车底板压力最小的是( )
(2004?淮安二模)卡车在行驶时,货物随车厢底板上下振动而不脱离底板,设货物作简谐运动.以竖直向上为正方向,其振动图象如图所示,则在图象上a、b、c、d四点中货物对车底板压力最小的是( )