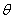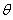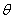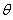题目内容
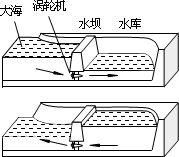
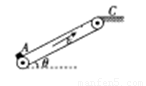
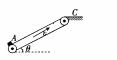
如图所示，传送带与水平方向成θ=30°角，皮带的AB部分长为L=3.25m，皮带以速度v=2m/s顺时针方向运动，在A端无初速地放上一质量为m=1kg的小物体，小物体与皮带间的动摩擦因数为μ=
，求：
（1）物体从A端到B端所需的时间，
（2）从A到B运动的过程中一共产生多少热量？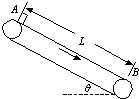
| ||
| 5 |
（1）物体从A端到B端所需的时间，
（2）从A到B运动的过程中一共产生多少热量？
（1）第一阶段：物体沿传送带向下做匀加速直线运动，则由牛顿第二定律得
mg sin30°+μmg cos30°=ma1，
得加速度为 a1=8 m/s2，
设加速到与传送带同速的时间为t1：v=a1t1
则得t1=0.25 s，
此过程物体的位移为 s1=0.25 m，皮带位移为s1′=vt1=0.5 m．
第二阶段：由于mgsinθ＞μFN=μmgcosθ，故物体继续沿传送带向下做匀加速直线运动
则有 mg sin30°-μmg cos30°=ma2，
得加速度为 a2=2 m/s2，
此过程通过的位移 s2=（3.25-0.25）m=3 m，
由s2=vt2+
a2t22，解得：t2=1 s，
总时间为t=t1+t2=1.5 s，皮带位移为s2′=vt2=2 m，
（2）从A到B运动的过程中一共产生的热量为 Q=f△s1+f△s2=f（s1′-s1）+f（s2′-s2）=3.75 J．
答：
（1）物体从A端到B端所需的时间是1.5s，
（2）从A到B运动的过程中一共产生3.75J的热量．
mg sin30°+μmg cos30°=ma1，
得加速度为 a1=8 m/s2，
设加速到与传送带同速的时间为t1：v=a1t1
则得t1=0.25 s，
此过程物体的位移为 s1=0.25 m，皮带位移为s1′=vt1=0.5 m．
第二阶段：由于mgsinθ＞μFN=μmgcosθ，故物体继续沿传送带向下做匀加速直线运动
则有 mg sin30°-μmg cos30°=ma2，
得加速度为 a2=2 m/s2，
此过程通过的位移 s2=（3.25-0.25）m=3 m，
由s2=vt2+
| 1 |
| 2 |
总时间为t=t1+t2=1.5 s，皮带位移为s2′=vt2=2 m，
（2）从A到B运动的过程中一共产生的热量为 Q=f△s1+f△s2=f（s1′-s1）+f（s2′-s2）=3.75 J．
答：
（1）物体从A端到B端所需的时间是1.5s，
（2）从A到B运动的过程中一共产生3.75J的热量．
练习册系列答案
名校课堂系列答案
相关题目
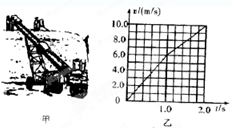如图所示为一皮带传送装置，皮带保持匀速率运动，货物由静止放到传送带上，被传送带向下传送，其运动的v-t图象如图乙所示．
，货物所受的最大静摩擦力等于滑动摩擦力，传送带斜面的长度为L。若皮带的倾角
、运行速度秒和货物的质量m都可以调节(