Question

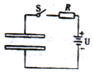
如图所示，水平放置的平行金属板A、B与电源相连，开关S闭合，一个带电质点从P点自由下落，恰好从两板正对的小孔M射入，到小孔N时速度刚好为零，然后返回，若要使质点仍从P点自由下落，最终穿过N孔继续下落，可行的办法是（　　）

A．将A板向下平移一小段距离

B．将A板向上平移一小段距离

C．断开开关S，再把B板向下平移一小段距离

D．断开开关S，再把B板向上平移一小段距离

Answer 1

设质点距离A板的高度h，A、B两板原来的距离为d，电压为U．质点的电量为q．
A、B由题质点到达b孔时速度恰为零，根据动能定理得mg（h+d）-qU=0．若保持S闭合，将A板适当上移或下移，设质点到达b时速度为v，由动能定理得mg（h+d）-qU=

1

2

mv2，v=0，说明质点到达N孔时速度恰为零，然后返回，不能穿过N孔．故AB错误．
C、若断开S，再将B板适当下移，板间电场强度不变，设质点进入电场的深度为d′时速度为零．根据动能定理可知，mg（h+d′）-qEd′=0，又由原来情况有mg（h+d）-qEd=0．比较两式得，d′=d，说明质点到达N孔原来的位置速度减为零，则质点不能穿过N孔．故C错误．
D、由C分析得知，把B板向上平移一小段距离时，板间电场强度不变，质点到达N孔时有向下的速度，可穿过N孔继续下落．故D正确．
故选D