题目内容
火星有两颗卫星,分别是火卫一和火卫二,它们的轨道近似为圆。已知火卫一的周期为7小时39分。火卫二的周期为30小时18分,则两颗卫星相比
| A.火卫一距火星表面较近。 | B.火卫二的质量较大 |
| C.火卫二运动速度较大。 | D.火卫二的向心加速度较大 |
A
根据卫星的万有引力等于向心力,列式求出线速度、角速度、周期和向心力的表达式进行讨论即可.卫星绕火星做匀速圆周运动,根据万有引力提供向心力,设卫星的质量为m、轨道半径为r、火星质量为M,有
F=F向

F向=m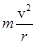 =mω2r=m(
=mω2r=m(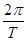 )2r
)2r
因而
 =
=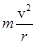 =mω2r= m(
=mω2r= m(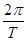 )2r =ma
)2r =ma
解得
v= ①
①
T= =2π
=2π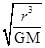 ②
②
ω= ③
③
a= ④
④
由于火卫二周期较大,根据②式,其轨道半径较大,再结合①③④式,可知火卫二的线速度较小、角速度较小、加速度较小;
点评:本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.
F=F向

F向=m
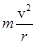 =mω2r=m(
=mω2r=m(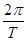 )2r
)2r因而
 =
=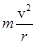 =mω2r= m(
=mω2r= m(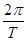 )2r =ma
)2r =ma解得
v=
 ①
①T=
 =2π
=2π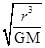 ②
②ω=
 ③
③a=
 ④
④由于火卫二周期较大,根据②式,其轨道半径较大,再结合①③④式,可知火卫二的线速度较小、角速度较小、加速度较小;
点评:本题关键抓住万有引力提供向心力,列式求解出线速度、角速度、周期和向心力的表达式,再进行讨论.

练习册系列答案
相关题目
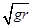
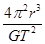
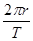
 ,
, 卫星离地面的高度等于
卫星离地面的高度等于 卫星离地面高度为
卫星离地面高度为 ,则:
,则:
 是多少?
是多少?
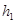 和
和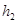 ,运动的向心加速度分别是
,运动的向心加速度分别是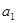 和
和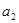 ,运动周期分别为
,运动周期分别为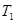 和
和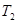 。已知月球半径为R,则
。已知月球半径为R,则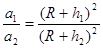 ,
,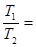
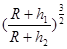
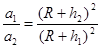 ,
,