题目内容
2. 如图所示,物体沿一曲面从A点无初速度滑下,滑至曲面最低点B时,下滑的高度为5m.若物体的质量为1㎏,到B点的速度为6m/s,则在下滑过程中阻力对物体所做的功是多少?(取g=10m/s2)
如图所示,物体沿一曲面从A点无初速度滑下,滑至曲面最低点B时,下滑的高度为5m.若物体的质量为1㎏,到B点的速度为6m/s,则在下滑过程中阻力对物体所做的功是多少?(取g=10m/s2)
分析 对A到B的过程运用动能定理,求出下滑过程中阻力做功的大小.
解答 解:从A到B设阻力做功Wf 由动能定理得:
mgh+Wf=$\frac{1}{2}$mv2-0
代入数据得:Wf=-32 J
答:在下滑过程中阻力对物体所做的功是-32J.
点评 运用动能定理解题关键选择好研究的过程,分析过程中有哪些力做功,然后根据动能定理列式求解,基础题.

练习册系列答案
相关题目
12.一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度-时间(vx-t)图象和y方向的位移-时间(y-t)图象分别如图乙、丙所示,由此可知( )


| A. | t=0s时,质点的速度大小为12m/s | B. | 质点做加速度恒定的曲线运动 | ||
| C. | 前两秒,质点所受的合力大小为10N | D. | t=1.0s时,质点的速度大小为7m/s |
10. 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
 某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )
某变速箱中有甲、乙、丙三个齿轮,如图所示,其半径分别为r1、r2、r3,若甲轮匀速转动的角速度为ω,三个轮相互不打滑,则丙轮边缘上各点的向心加速度大小为( )| A. | $\frac{{{r}_{1}}^{2}{ω}^{2}}{{r}_{3}}$ | B. | $\frac{{{r}_{3}}^{2}{ω}^{2}}{{{r}_{1}}^{2}}$ | C. | $\frac{{{r}_{3}}^{3}{ω}^{2}}{{{r}_{1}}^{2}}$ | D. | $\frac{{r}_{1}{r}_{2}{ω}^{2}}{{r}_{3}}$ |
17.一质量为m的物体静止在粗糙的水平面上,当此物体在水平拉力作用下运动时其动能为E1,若水平拉力为第一次的2倍,此物体静止开始运动相同的距离s其动能为E2,则( )
| A. | E2等于E1 | B. | E2等于2E1 | ||
| C. | E2大于2E1 | D. | E2大于E1而小于2E1 |
14. 如图所示,一根有质量的金属棒MN,两端用细软导线连接后悬挂于a、b两点.棒的中部处于方向垂直纸面向里的匀强磁场中,棒中通有电流,方向从M流向N,此时悬线上有拉力,为了使拉力等于零,可( )
如图所示,一根有质量的金属棒MN,两端用细软导线连接后悬挂于a、b两点.棒的中部处于方向垂直纸面向里的匀强磁场中,棒中通有电流,方向从M流向N,此时悬线上有拉力,为了使拉力等于零,可( )
 如图所示,一根有质量的金属棒MN,两端用细软导线连接后悬挂于a、b两点.棒的中部处于方向垂直纸面向里的匀强磁场中,棒中通有电流,方向从M流向N,此时悬线上有拉力,为了使拉力等于零,可( )
如图所示,一根有质量的金属棒MN,两端用细软导线连接后悬挂于a、b两点.棒的中部处于方向垂直纸面向里的匀强磁场中,棒中通有电流,方向从M流向N,此时悬线上有拉力,为了使拉力等于零,可( )| A. | 适当减小磁感应强度 | B. | 使磁场反向 | ||
| C. | 适当增大电流强度 | D. | 使电流反向 |
16. 一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
 一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )
一根弹性绳上有两个波源S1和S2,P点为两个波源连线的中点,两个波源同时起振各自发出一个脉冲波如图所示,已知两个脉冲波的频率分别为f1和f2(f1<f2),振幅分别A1和A2(A1<A2),下列说法中正确的是( )| A. | 两列波相遇后,各自独立传播 | |
| B. | 两列波同时传播到P点 | |
| C. | 波源S1,S2的起振方向相反 | |
| D. | 两列波相遇过程中,P点振幅可达(A1+A2) |
17.某卫星绕地球做匀速圆周运动的线速度大小为v,已知地球半径为R,地球表面重力加速度为g,该卫星的轨道半径为( )
| A. | $\root{3}{\frac{{v}^{2}}{g{R}^{2}}}$ | B. | $\frac{g{R}^{2}}{{v}^{2}}$ | C. | $\frac{{v}^{2}}{g{R}^{2}}$ | D. | $\root{3}{\frac{g{R}^{2}}{{v}^{2}}}$ |
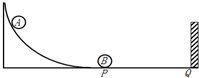 如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,小球B静止在水平地面上,B离竖直墙的距离是PQ=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,也不计B与墙碰撞时间,在离墙2.5m处两球发生第二次碰撞,重力加速度g=10m/s2,求:
如图所示,质量为0.3kg的小球A放在光滑的曲面上,离地面的高度0.2m,小球B静止在水平地面上,B离竖直墙的距离是PQ=3.5m,A静止释放,与B发生弹性碰撞,B与墙碰撞无机械能损失,也不计B与墙碰撞时间,在离墙2.5m处两球发生第二次碰撞,重力加速度g=10m/s2,求: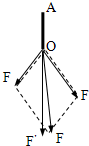 某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结合点,图中F是F1、F2合力的理论值,F′是合力的实验值,通过本实验,可以得出结论:在误差允许的范围内平行四边形定则是正确的.
某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结合点,图中F是F1、F2合力的理论值,F′是合力的实验值,通过本实验,可以得出结论:在误差允许的范围内平行四边形定则是正确的.