题目内容
18.如图所示,小物块位于半径为R的半球形物体顶端,若给小物块一水平速度v0=√2gR√2gR,则物块( )
| A. | 沿球体表面做圆周运动 | B. | 落地时水平位移为√2R√2R | ||
| C. | 落地速度大小为√gR√gR | D. | 落地时速度方向与地面成45°角 |
分析 在最高点,物体沿半径方向的合力提供向心力,根据牛顿第二定律判断是否有支持力,从而判断物体的运动情况.
解答 解:在最高点,当支持力为零时,根据牛顿第二定律得:
mg=mv2Rv2R
解得:v=√gR√gR
因为vo=√2gR>√gR
所以小物块将立即做平抛运动,
根据动能定理得:12mv′2−12mv20=mgR
解得落地时速度为:v′=2√gR
设落地时速度方向与地面成θ角,则:
cosθ=v0v′=√2gR2√gR=√22
故θ=45°,故ABC错误,D正确.
故选:D.
点评 解决本题的关键知道圆周运动径向的合力提供向心力.以及知道仅受重力,有水平初速度将做平抛运动.

练习册系列答案
相关题目
8.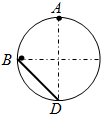 如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )
如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )
 如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )
如图所示,将小球甲、乙(都可视为质点)分别从A、B两点由静止同时释放,最后都到达竖直面内圆弧的最低点D,其中甲是从A出发做自由落体运动,乙沿弦轨道从一端B到达另一端D.如果忽略一切摩擦阻力,那么下列判断正确的是( )| A. | 甲、乙同时到达D点 | B. | 甲球最先到达D点 | ||
| C. | 乙球最先到达D点 | D. | 无法判断哪个球先到达D点 |
9.如图所示是甲、乙两物体做匀速直线运动的位移-时间图象,则下列说法中错误的是( )


| A. | 甲开始运动时刻比乙早t1 | B. | 当t=t2时,两物体相遇 | ||
| C. | 当t=t2时,两物体相距最远 | D. | 当t=t3时,两物体相距X1 |
13.一个实心铁球与一实心木球质量相等,将它们放在同一水平地面上,下列结论中正确的是(选地面为参考平面)( )
| A. | 铁球的重力势能大于木球的重力势能 | |
| B. | 铁球的重力势能等于木球的重力势能 | |
| C. | 铁球的重力势能小于木球的重力势能 | |
| D. | 上述三种情况都有可能 |
3.关于斜上抛运动,下列说法中正确的是( )
| A. | 是匀变速运动 | B. | 最高点速度为0 | ||
| C. | 水平方向的分运动是平抛运动 | D. | 竖直方向的分运动是竖直上抛运动 |
10.下列关于布朗运动的说法中,正确的是( )
| A. | 布朗运动就是液体分子的无规则运动 | |
| B. | 布朗运动就是悬浮粒子的分子的无规则运动 | |
| C. | 布朗运动就是悬浮粒子的运动 | |
| D. | 布朗运动就是分子热运动 |


 在平抛物体运动的实验中
在平抛物体运动的实验中