题目内容
质量为M的小车置于水平面上.小车的上表面由1/4圆弧和平面组成,车的右端固定有一不计质量的弹簧,圆弧AB部分光滑,半径为R,平面BC部分粗糙,长为l,C点右方的平面光滑.滑块质量为m,从圆弧最高处A无初速下滑(如图),与弹簧相接触并压缩弹簧,最后又返回到B相对于车静止.求:
(1)BC部分的动摩擦因数μ;
(2)弹簧具有的最大弹性势能;
(3)当滑块与弹簧刚分离时滑块和小车的速度大小.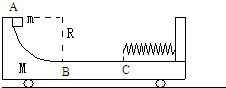
(1)BC部分的动摩擦因数μ;
(2)弹簧具有的最大弹性势能;
(3)当滑块与弹簧刚分离时滑块和小车的速度大小.

(1)滑块与小车初始状态为静止,末状态滑块相对小车静止,即两者共速且速度为0,
据能量守恒:
mgR=μmg?2l,
∴μ=
(2)弹簧压缩到最大形变量时,滑块与小车又一次共速,且速度均为0,此时据能量守恒,
弹簧的弹性势能EP=mgR-μmgl=
(3)弹簧与滑块分离的时候,弹簧的弹性能为0,设此时滑块速度为v1,小车速度为v2据能量守恒有:
EP=
m
+
M
又因为系统动量守恒,有:mv1-Mv2=0
解得:v1=
v2=
答:(1)BC部分的动摩擦因数μ=
;
(2)弹簧具有的最大弹性势能是
;
(3)当滑块与弹簧刚分离时滑块和小车的速度大小分别是v1=
,v2=
.
据能量守恒:
mgR=μmg?2l,
∴μ=
| R |
| 2l |
(2)弹簧压缩到最大形变量时,滑块与小车又一次共速,且速度均为0,此时据能量守恒,
弹簧的弹性势能EP=mgR-μmgl=
| mgR |
| 2 |
(3)弹簧与滑块分离的时候,弹簧的弹性能为0,设此时滑块速度为v1,小车速度为v2据能量守恒有:
EP=
| 1 |
| 2 |
| v | 21 |
| 1 |
| 2 |
| v | 22 |
又因为系统动量守恒,有:mv1-Mv2=0
解得:v1=
|
v2=
| m |
| M |
|
答:(1)BC部分的动摩擦因数μ=
| R |
| 2l |
(2)弹簧具有的最大弹性势能是
| mgR |
| 2 |
(3)当滑块与弹簧刚分离时滑块和小车的速度大小分别是v1=
|
| m |
| M |
|

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目





 ,
, ,
, ,
, ,
, ,
,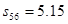 cm。试问:
cm。试问:
 = m/s(结果保留2位有效数字);若滴水的周期为T,则小车的加速度
= m/s(结果保留2位有效数字);若滴水的周期为T,则小车的加速度 =
(用英文符号表示)。
=
(用英文符号表示)。




 、
、 ,并测出间距d 。开始时让木板置于
,并测出间距d 。开始时让木板置于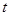 。
。
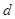 、
、 = ;为了减小测量加速度的偶然误差可以采用的方法是(一种即可) 。
= ;为了减小测量加速度的偶然误差可以采用的方法是(一种即可) 。 