题目内容
【题目】如图,两个弹性小球a和b的质量分别为ma、mb . a球原来静止在离地高度H=2.4m的P点,b球原来静止在离地高度h=1.6m的Q点,先静止释放a球,在a球即将碰到b球时同样静止释放b球,两球碰撞时间极短,碰后在同一竖直线运动,己知mb=3ma , 重力加速度大小g=10m/s2 , 忽略小球大小、空气阻力及碰撞中的动能损失,且小球落地后不再跳起,求:
(1)a球即将碰到b球时速度;
(2)b球与a球先后落地的时间差.
【答案】
(1)解:a下落的过程中有:△h=H﹣h=2.4﹣1.6=0.8m
a球即将碰到b球时速度为:v= ![]() m/s
m/s
答: a球即将碰到b球时速度是4m/s;
(2)解:a与b碰撞的瞬间可以认为竖直方向的动量守恒,选择向下为正方向,得:
mav=mav1+mbv2
忽略小球大小及碰撞中的动能损失得:
![]()
联立得:v1=﹣2m/s,负号表示方向向上;v2=2m/s
碰撞后a做竖直上抛运动,则:
![]()
b做竖直下抛运动,则:
![]()
二者的时间差:△t=t1﹣t2
联立得:t1=0.8s,t2=0.4s,△t=0.4s
答:b球与a球先后落地的时间差是0.4s.
【解析】本题考察动量守恒定律的应用,理解动量守恒的条件,选择正确的公式列方程求解即可。
【考点精析】解答此题的关键在于理解动能定理的综合应用的相关知识,掌握应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷,以及对动量守恒定律的理解,了解动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变.

【题目】橡皮筋也像弹簧一样,在弹性限度内,伸长量x与弹力F成正比,即F=kx,k的值与橡皮筋未受到拉力时的长度L、横截面积S有关,理论与实践都表明k=YS/L,其中Y是一个由材料决定的常数,材料力学中称之为杨氏模量.

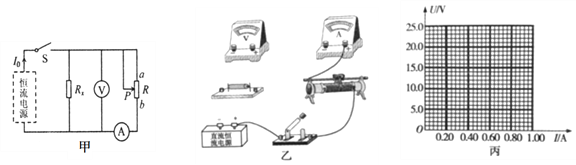
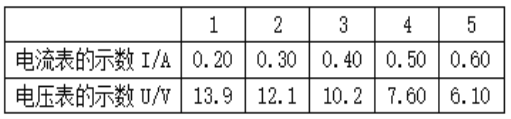
(1)有一段横截面是圆形的橡皮筋,应用如图甲所示的实验装置可以测量出它的杨氏模量Y的值.下表为橡皮筋受到的拉力F与伸长量x的实验记录,请在图乙中作出F-x图象_____.
拉力F/N | 5.0 | 10.0 | 15.0 | 20.0 | 25.0 |
伸长量x/cm | 1.60 | 3.20 | 4.80 | 6.40 | 8.00 |
(2)由以上实验可求出该橡皮筋的K值为________N/m(保留两位有效数字).

(3)某同学在家中用三根相同的橡皮筋(遵循胡克定律)来探究合力的方法,如图所示,三根橡皮筋在O点相互连接,拉长后三个端点用图钉固定在A、B、C三点.在实验中,可以通过刻度尺测量橡皮筋的长度来得到橡皮筋的拉力大小,并通过OA、OB、OC的方向确定三个拉力的方向,从而探究求其中任意两个拉力的合力的方法.在实验过程中,下列说法正确的是(____)
A.只需要测量橡皮筋的长度,不需要测出橡皮筋的原长
B.为减小误差,应选择劲度系数尽量大的橡皮筋
C.以OB、OC为两邻边作平行四边形,其对角线必与OA在一条直线上且长度与OA相等
D.多次实验中即使O点不固定,也可以探究求合力的方法