题目内容
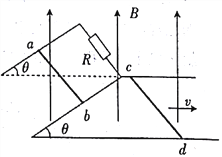
【题目】如图所示，间距为L=1m的两条足够长的平行金属导轨与水平面的夹角为θ=37°，底端用电阻为R=0.8Ω的导体MN相连接，导轨电阻忽略不计．磁感应强度为B=1T的匀强磁场与导轨平面垂直，磁场区域上下边界距离为d=0.85m，下边界aa′和导轨底端相距为3d．一根质量为m=1kg、电阻为r=0.2Ω的导体棒放在导轨底端，与导轨垂直且接触良好，并以初速度v0 = 10m/s沿斜面向上运动，到达磁场上边界bb′时，恰好速度为零．已知导轨与棒之间的动摩擦因数为μ=0.5，g=10m/s2，sin37°=0.6，cos37°=0.8．求：
（1）导体棒通过磁场过程中产生的焦耳热；
（2）导体棒从进入磁场到达上边界所用的时间和回路中产生的感应电流的有效值；
（3）微观上导体中的电子克服因碰撞产生的阻力做功，宏观上表现为产生焦耳热．试从微观角度推导：当棒运动到磁场中某一位置时(感应电流为I)，其电阻的发热功率为P热 =I2r（推导过程用字母表示）
【答案】(1)Q=16J (2) t=0.615s 故I=
A
5A (3)见解析
【解析】试题分析：（1）根据能量守恒定律即可求解产生的热量；（2）根据动能定理求出到达上边界的速度，根据动量定理求解所用的时间，根据
求出电流；（3）根据瞬时功率的表达式和电流的微观表达式进行分析。
(1)这一过程中，棒的动能转化为重力势能和摩擦生热以及焦耳热Q
由能量守恒得：
解得:
代入数据，解得Q=16J
(2) 棒从开始到运动到磁场边界，由动能定理得：
解得
在棒向上通过磁场的过程中，选沿斜面向下为正，由动量定理得：
又
，
解得t=0.615s
又
故
A
(3)设导体棒中单位体积的电子数为n，导体棒的横截面积为S
则导体棒中的总电子数
当棒运动到磁场中某一位置时，设电子相对导线定向移动的速率为
则导体棒中所有电子克服阻力做功的功率
当棒运动到磁场中某一位置时，设棒的速度大小为
，棒两端电压为U。在棒运动到磁场中某一位置时的极短时间内，可认为电流不变，电子相对导线定向移动的速率为不变，则棒中某个电子受力在这一瞬时受力平衡，故受的阻力
又
导体棒中所有电子克服阻力做功的功率
，等于棒中电阻的发热功率
，即
联立得：
故
