题目内容
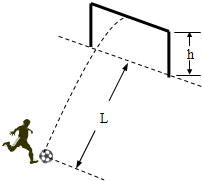
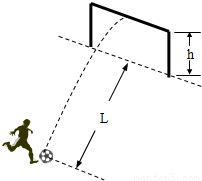
 一场精彩的足球赛,经过激烈鏖战终未分出胜负,最后进入点球大战.罚点球时,有一运动员飞起一脚将球踢飞,恰好击中横梁,守门员估计打在横梁上的足球速度约为v. 已知足球的质量为m,球门横梁的高度为h,罚球点到球门线的水平距离为L,重力加速度为g,空气阻力不计.求:
一场精彩的足球赛,经过激烈鏖战终未分出胜负,最后进入点球大战.罚点球时,有一运动员飞起一脚将球踢飞,恰好击中横梁,守门员估计打在横梁上的足球速度约为v. 已知足球的质量为m,球门横梁的高度为h,罚球点到球门线的水平距离为L,重力加速度为g,空气阻力不计.求:(1)足球被踢出时的速度约为多大?
(2)运动员踢球时对球所做的功约为多少?
分析:(1)不计空气阻力,足球在飞行过程中,只有重力做功,机械能守恒,由机械能守恒定律列式求足球被踢出时的速度;
(2)对运动员踢球过程,根据动能定理列式求解运动员对足球做的功.
(2)对运动员踢球过程,根据动能定理列式求解运动员对足球做的功.
解答:解:(1)足球从被踢出到打在横梁上的过程中,由机械能守恒定律得:
m
=
mv2+mgh
解之得:足球被踢出时的速度 v0=
(2)对踢球过程,由动能定理得:W=
m
=
mv2+mgh
答:
(1)足球被踢出时的速度约为
.
(2)运动员踢球时对球所做的功约为
m
+mgh.
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
解之得:足球被踢出时的速度 v0=
| v2+2gh |
(2)对踢球过程,由动能定理得:W=
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
答:
(1)足球被踢出时的速度约为
| v2+2gh |
(2)运动员踢球时对球所做的功约为
| 1 |
| 2 |
| v | 2 0 |
点评:本题踢球过程中,运动员的作用力是变力,运用动能定理求变力的功是常用的方法.

练习册系列答案
相关题目
 如图所示,在水平向右场强为E的匀强电场中,有一质量为m、电荷量为q的占由荷从A点由静止释放,仅在由场力的作用下经时间t运动到B点.求.
如图所示,在水平向右场强为E的匀强电场中,有一质量为m、电荷量为q的占由荷从A点由静止释放,仅在由场力的作用下经时间t运动到B点.求.