题目内容
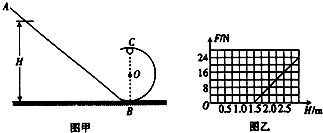 在半径R=4800km的某星球表面.宇航员做了如下实验,实脸装置如圈甲所示.竖直平面内的光滑轨道由AB和圈孤轨道BC组成.将质量 m=1.0kg的小球,从轨道AB上高H处的某点静止滑下,用力传感骼侧出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小.F随H的变化关系如图乙所示.求:
在半径R=4800km的某星球表面.宇航员做了如下实验,实脸装置如圈甲所示.竖直平面内的光滑轨道由AB和圈孤轨道BC组成.将质量 m=1.0kg的小球,从轨道AB上高H处的某点静止滑下,用力传感骼侧出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F大小.F随H的变化关系如图乙所示.求:(1)回轨道的半径,
(2)该星球的第一宇宙速度.
分析:(1)小球从A到C运动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律和牛顿第二定律求出小球对轨道C点的压力与H的关系式,然后结合F-H图线求出圆轨道的半径和星球表面的重力加速度.
(2)当卫星在星球表面附近做匀速圆周运动时,重力提供向心力,其速度即为第一宇宙速度,由牛顿第二定律求解.
(2)当卫星在星球表面附近做匀速圆周运动时,重力提供向心力,其速度即为第一宇宙速度,由牛顿第二定律求解.
解答:解:(1)小球过C点时满足
F+mg=m
从A到C运动的过程中,只有重力做功,机械能守恒,则有
mg(H-2r)=
mυC2
联立解得 F=
H-5mg
由题图可知 H1=1.5 m时F1=0;H2=2.0 m时F2=8 N
可解得 g=4.8 m/s2
r=0.6 m
(2)当m
=mg时,v=
=4.8km/h
即该星球的第一宇宙速度是4.8km/h
答:(1)圆轨道的半径为0.6m.
(2)该星球的第一宇宙速度是4.8km/h.
F+mg=m
| ||
| r |
从A到C运动的过程中,只有重力做功,机械能守恒,则有
mg(H-2r)=
| 1 |
| 2 |
联立解得 F=
| 2mg |
| r |
由题图可知 H1=1.5 m时F1=0;H2=2.0 m时F2=8 N
可解得 g=4.8 m/s2
r=0.6 m
(2)当m
| v2 |
| R |
| gR |
即该星球的第一宇宙速度是4.8km/h
答:(1)圆轨道的半径为0.6m.
(2)该星球的第一宇宙速度是4.8km/h.
点评:点评:本题是牛顿运动定律与机械能守恒定律的综合题,解决本题的关键根据该规律得出压力F与H的关系式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=11cm的圆形范围内,水面上的运动员手到脚的长度l=10cm.若已知水的折射率n=
如图是北京奥运会期间安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=11cm的圆形范围内,水面上的运动员手到脚的长度l=10cm.若已知水的折射率n=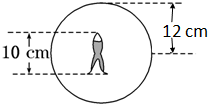 如图所示是伦敦奥运会期间水上运动中心安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=12cm的圆形范围内,水面上的运动员手到脚的长度l=10cm.若已知水的折射率
如图所示是伦敦奥运会期间水上运动中心安置在游泳池底部的照相机拍摄的一张照片,相机的镜头竖直向上.照片中,水立方运动馆的景象呈现在半径r=12cm的圆形范围内,水面上的运动员手到脚的长度l=10cm.若已知水的折射率