题目内容
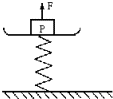
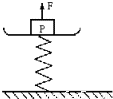
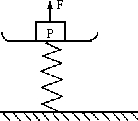
如图,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止.P的质量为12 kg,弹簧的劲度系数k=800 N/m.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动.已知在前0.2 s内F是变化的,在0.2 s以后F是恒力,则F的最小值是多少,最大值是多少?
答案:
解析:
解析:
|
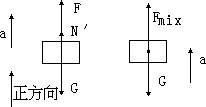
正确解答:解题的关键是要理解0.2s前F是变力,0.2s后F是恒力的隐含条件.即在0.2s前物体受力和0.2s以后受力有较大的变化. 以物体P为研究对象.物体P静止时受重力G、称盘给的支持力N. 因为物体静止,∑F=0 N=G=0 ① N=kx0 ② 设物体向上匀加速运动加速度为a. 此时物体P受力如图受重力G,拉力F和支持力
据牛顿第二定律有 F+ 当0.2 s后物体所受拉力F为恒力,即为P与盘脱离,即弹簧无形变,由0~0.2 s内物体的位移为x0.物体由静止开始运动,则 将式①,②中解得的x0=0.15 m代入式③解得a=7.5 m/s2 F的最小值由式③可以看出即为 代入式③得 Fmin=ma+mg-kx0 =12×(7.5+10)-800×0.15=90(N) F最大值即N=0时,F=ma+mg=210(N) 小结:本题若称盘质量不可忽略,在分析中应注意P物体与称盘分离时,弹簧的形变不为0,P物体的位移就不等于x0,而应等于x0-x(其中x即称盘对弹簧的压缩量). |

练习册系列答案
相关题目
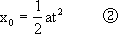
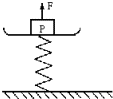 如图,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止.P的质量为12kg,弹簧的劲度系数k=800N/m.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动.已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?
如图,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止.P的质量为12kg,弹簧的劲度系数k=800N/m.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动.已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?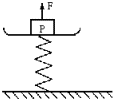 如图,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止.P的质量为12kg,弹簧的劲度系数k=800N/m.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动.已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?
如图,一个弹簧台秤的秤盘质量和弹簧质量都可以不计,盘内放一个物体P处于静止.P的质量为12kg,弹簧的劲度系数k=800N/m.现给P施加一个竖直向上的力F,使P从静止开始向上做匀加速运动.已知在前0.2s内F是变化的,在0.2s以后F是恒力,则F的最小值是多少,最大值是多少?