题目内容
如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，将两个电荷量都为q的正、负点电荷放在圆周上，它们的位置关于AC对称，距离等于圆的半径．要使圆心O处的电场强度为零，可在圆周上再放置一个电荷量和位置分别为（ ）分析：根据电场的叠加，先求出两个点电荷在0点的合场强大小和方向，在根据电场的叠加确定第三个点电荷．
解答：解：两个点电荷在0点产生的场强大小都为k
两个场强的方向互成120°，根据平行四边形定则，合场强大小为k
，方向水平向右．
所以最后一个电荷在O点产生的场强大小为k
，方向水平向左．所以该电荷若在B点，为-q，若在D点，为+q．故B、D正确，A、C错误．
故选BD．
| q |
| r2 |
| q |
| r2 |
所以最后一个电荷在O点产生的场强大小为k
| q |
| r2 |
故选BD．
点评：解决本题的关键掌握点电荷的场强公式E=k
，以及会利用平行四边形定则进行合成．
| q |
| r2 |
练习册系列答案
名校通行证有效作业系列答案
相关题目
如图所示，AC和BD为竖直方向的两根很长的平行光滑导轨．导轨间距L=0.5m，电阻不计，接在A、B间的定值电阻R=0.9Ω．两导轨间存在垂直于纸面向里的匀强磁场．一根质量m=0.25kg，电阻r=0.1Ω的光滑金属杆MN从静止开始下滑，下滑过程中，金属杆始终垂直于导轨并与导轨保持良好接触，其v-t图象如图所示，求磁场的磁感应强度B的大小．
如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，将等电量的正、负点电荷放在圆周上BD两点，下列说法正确的是（ ）
如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，半径为R．电荷量均为Q的正、负点电荷放在圆周上，它们的位置关于AC对称°°下列说法正确的是（ ）
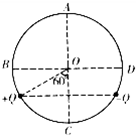如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，半径为R．电荷量均为Q的正、负点电荷放在圆周上，它们的位置关于AC对称，+Q与O点的连线和OC间夹角为60°．下列说法正确的是（ ）| A、O、C两点场强相同 | B、O、C两点电势相同 | C、在A点由静止释放一个正电荷，电荷将沿圆周向D运动 | D、沿直径由B向D移动一个正电荷，电荷的电势能先增大后减小 |