Question

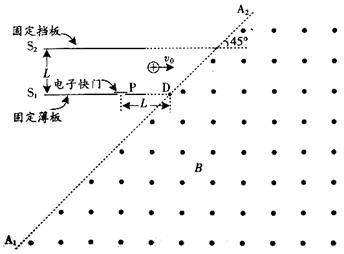
如图所示是某装置的垂直截面图，虚线A₁A₂是垂直截面与磁场区边界面的交线，匀强磁场分布在A₁A₂的右侧区域，磁感应强度B=0.4T，方向垂直纸面向外，A₁A₂与垂直截面上的水平线夹角为45⁰。在A₁A₂左侧，固定的薄板和等大的挡板均水平放置，它们与垂直截面交线分别为S₁、S₂，相距L=0.2m.。在薄板上P处开一个小孔，P与A₁A₂线上点D的水平距离为L。在小孔处装一个电子快门。起初快门开启，一旦有带正电微粒刚通过小孔，快门立即关闭。此后每隔T=开启一次并瞬间关闭。从S₁S₂之间的某一位置水平发射一速度为的带电微粒，它经过磁场区域后入射到P处小孔。通过小孔的微粒与挡板发生碰撞而反弹，反弹速度大小是碰前的0.5倍。

    （1）经过一次反弹直接从小孔射出的微粒，其初速度应为多少？

    （2）求上述微粒从最初水平射入磁场到第二次离开磁场的时间。（忽略微粒所受重力影响，碰撞过程无电荷转移。已知微粒的荷质比。只考虑纸面上带电微粒的运动。）

   

Answer 1

v₀=100m/s     

解析:

樊守青（1）如图所示，设带下电微粒在S₁S₂之间任意点Q以水平速度v₀进入磁场，微粒受到洛仑兹力为f，在磁场中做圆周运动的半径为r，有f=qv₀B

    

    解得：

    欲使微粒能进入小孔，半径r的取值范围为：

    L<r<2L

    代入数据得：

    80m/s<v₀<160m/s

    欲使进入小孔的微粒与挡板一次相碰返回后能通过小孔，还必须满足条件：

    ，其中n=1，2，3，……

    联立解得，v₀=100m/s

    (2)设微粒在磁场中做圆周运动的周期为T₀，从水平进入磁场到第二次离开磁场的总时间为t，设t₁、t₄分别为带电微粒第一次、第二次在磁场中运动的时间，第一次离开磁场运动到挡板的时间为t₂，碰撞后再返回到磁场的时间为t₃，运动轨迹如图所示。则有：

    ，，，，，