题目内容
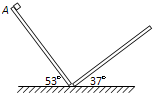 一位同学在水平桌面上用两块相同的木板搭了两个倾角分别为53°和37°的斜面,并使两个斜面之间平滑连接.两木板的长度均为L=0.60m,如图所示.让一个小滑块(可视为质点)从左边斜面顶端A由静止开始下滑,滑块在另一斜面上速度减为零时,恰好位于该斜面长度一半的位置.忽略滑块经过木板连接处时的能量损失.已知木板的质量与滑块的质量之比为3:1,sin53°=0.80,cos53°=0.60,重力加速度g取10m/s2.
一位同学在水平桌面上用两块相同的木板搭了两个倾角分别为53°和37°的斜面,并使两个斜面之间平滑连接.两木板的长度均为L=0.60m,如图所示.让一个小滑块(可视为质点)从左边斜面顶端A由静止开始下滑,滑块在另一斜面上速度减为零时,恰好位于该斜面长度一半的位置.忽略滑块经过木板连接处时的能量损失.已知木板的质量与滑块的质量之比为3:1,sin53°=0.80,cos53°=0.60,重力加速度g取10m/s2.
(1)若将右边木板平放在桌面上并将其固定,让滑块仍然从左边斜面顶端由静止下滑,那么滑块离开水平木板时的速度为多大?
(2)若将右边的木板平放在桌面上,且忽略桌面与该木板间的摩擦,让滑块仍然从左边固定斜面的顶端由静止下滑,那么当滑块和右边木板具有相同的速度时,滑块相对于右边木板滑行的距离为多大?
解:(1)设滑块的质量为m.根据动能定理得
第一种情形:mgLsin53°-μmgcos53°L-mg Lsin37°-μmgcos37°
Lsin37°-μmgcos37°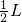 =0
=0
第二情形:设滑块离开水平木板时的速度为v.
mgLsin53°-μmgcos53°L-μmgL=
联立上两式得:μ=0.5,v=0
(2)设滑块滑到A板底端时速度大小为v1,滑块和右边木板具有的相同速度为v2.
根据动能定理得:mgLsin53°-μmgcos53°L=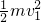
由动量守恒定律得:mv1=(m+3m)v2,
由能量守恒定律得: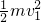 =μmgS+
=μmgS+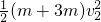
联立以上三式得 滑块相对于右边木板滑行的距离S=0.45m
答:
(1)滑块离开水平木板时的速度为0.
(2)滑块相对于右边木板滑行的距离为0.45m.
分析:(1)根据动能定理分别对两种情况全过程列式,联立可求出滑块离开水平木板时的速度.
(2)先求出滑块滑到A板底端时速度大小.滑块在左板上滑行时,系统的动量守恒,能量也守恒,根据两大守恒定律列式求出滑块相对于右边木板滑行的距离.
点评:本题是多个对象,多个过程的问题,在分析物体运动过程的基础上,运用动能定理、动量守恒和能量守恒结合进行处理.
第一种情形:mgLsin53°-μmgcos53°L-mg
 Lsin37°-μmgcos37°
Lsin37°-μmgcos37°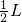 =0
=0第二情形:设滑块离开水平木板时的速度为v.
mgLsin53°-μmgcos53°L-μmgL=

联立上两式得:μ=0.5,v=0
(2)设滑块滑到A板底端时速度大小为v1,滑块和右边木板具有的相同速度为v2.
根据动能定理得:mgLsin53°-μmgcos53°L=
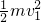
由动量守恒定律得:mv1=(m+3m)v2,
由能量守恒定律得:
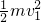 =μmgS+
=μmgS+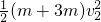
联立以上三式得 滑块相对于右边木板滑行的距离S=0.45m
答:
(1)滑块离开水平木板时的速度为0.
(2)滑块相对于右边木板滑行的距离为0.45m.
分析:(1)根据动能定理分别对两种情况全过程列式,联立可求出滑块离开水平木板时的速度.
(2)先求出滑块滑到A板底端时速度大小.滑块在左板上滑行时,系统的动量守恒,能量也守恒,根据两大守恒定律列式求出滑块相对于右边木板滑行的距离.
点评:本题是多个对象,多个过程的问题,在分析物体运动过程的基础上,运用动能定理、动量守恒和能量守恒结合进行处理.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
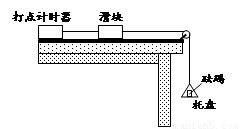
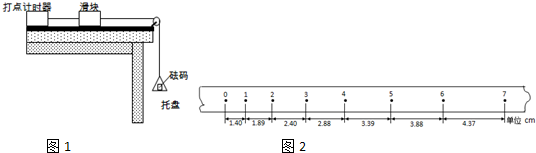
物理小组在一次探究活动中测量滑块做匀加速直线运动的加速度和某时刻的瞬时速度,实验装置如图,一木板固定在水平桌面上,一端装有定滑轮;木板上有一滑块,其一端与穿过电火花打点计时器的纸带相连,另一端通过跨过定滑轮的细线与托盘连接.打点计时器使用的交流电源的频率为50 Hz.开始实验时,在托盘中放入适量砝码,滑块开始做加速运动,在纸带上打出一系列小点. 

(1)结合本次实验,下列说法错误的是( )
| A.电火花打点计时器使用220V交流电源 |
| B.电火花打点计时器每隔0.02s打一个点 |
| C.实验中应先接通电源,等打点稳定后再释放滑块 |
| D.实验中应先释放滑块再打点 |
(3)某同学在实验中发现物体速度变化太慢,请你帮他想出一条能使速度变化加快的有效方案 。
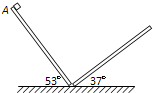 (2007?海淀区一模)一位同学在水平桌面上用两块相同的木板搭了两个倾角分别为53°和37°的斜面,并使两个斜面之间平滑连接.两木板的长度均为L=0.60m,如图所示.让一个小滑块(可视为质点)从左边斜面顶端A由静止开始下滑,滑块在另一斜面上速度减为零时,恰好位于该斜面长度一半的位置.忽略滑块经过木板连接处时的能量损失.已知木板的质量与滑块的质量之比为3:1,sin53°=0.80,cos53°=0.60,重力加速度g取10m/s2.
(2007?海淀区一模)一位同学在水平桌面上用两块相同的木板搭了两个倾角分别为53°和37°的斜面,并使两个斜面之间平滑连接.两木板的长度均为L=0.60m,如图所示.让一个小滑块(可视为质点)从左边斜面顶端A由静止开始下滑,滑块在另一斜面上速度减为零时,恰好位于该斜面长度一半的位置.忽略滑块经过木板连接处时的能量损失.已知木板的质量与滑块的质量之比为3:1,sin53°=0.80,cos53°=0.60,重力加速度g取10m/s2.