题目内容
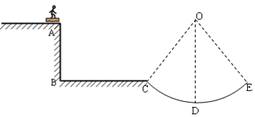
如图,滑板运动员在平台上从A位置水平滑出,在落到C位置时,运动员通过调整姿势进行缓冲使自己只保留沿圆轨道切向速度而不弹起。圆轨道光滑,O点为圆轨道圆心,C、E为等高点,OD为竖直线。已知:运动员与滑板的总质量M=90kg,AB=20m,BC=30m,
∠COE=600,g=10m/s2 ,cos27o=0.9996求:
(1)滑板运动员从A位置滑出时的速度大小。
(2)滑板运动员从E位置滑出时的速度大小(结果保留两位小数)。
(1)设滑板运动员从A位置滑出时的速度大小为Vo,从A位置滑至C位置的时间为t
BC=Vot ①
AB=![]() gt2 ②
gt2 ②
V0=15m/s ③
(2)设滑板运动员滑至C位置时速度大小为V1,运动员调整姿势后的速度为V2
mgAB=![]() mV12-
mV12-![]() mV02 ④
mV02 ④
V1=25m/s ⑤
设∠COD为α,V1与水平方向夹角为β,由几何关系得:
α=60o ⑥
β=53o ⑦
V2=V1cosβcosα+V1sinβsinα ⑧
V2=![]() m/s ⑨
m/s ⑨
设滑板运动员从E位置滑出时的速度大小为V2,根据机械能守恒定律,得:
V3=V2=24.82m/s ⑩
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目