题目内容
2. 如图,两根相距l=0.4m、电阻不计的平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连.导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T.一根质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=2m/s沿导轨向右运动,运动过程中电阻上消耗的功率不变.求:
如图,两根相距l=0.4m、电阻不计的平行光滑金属导轨水平放置,一端与阻值R=0.15Ω的电阻相连.导轨间x>0一侧存在沿x方向均匀增大的稳恒磁场,其方向与导轨平面垂直,变化率k=0.5T/m,x=0处磁场的磁感应强度B0=0.5T.一根质量m=0.1kg、电阻r=0.05Ω的金属棒置于导轨上,并与导轨垂直.棒在外力作用下从x=0处以初速度v0=2m/s沿导轨向右运动,运动过程中电阻上消耗的功率不变.求:(1)回路中的电流;
(2)金属棒在x=2m处的速度;
(3)金属棒从x=0运动到x=2m过程中安培力做功的大小;
(4)金属棒从x=0运动到x=2m过程中外力的平均功率.
分析 (1)由法拉第电磁感应定律与闭合电路欧姆定律相结合,来计算感应电流的大小;
(2)由因棒切割产生感应电动势,及电阻的功率不变,即可求解;
(3)分别求出x=0与x=2m处的安培力的大小,然后由安培力做功表达式,即可求解;
(4)依据功能关系,及动能定理可求出外力在过程中的平均功率.
解答 解:(1)金属棒切割产生感应电动势为:E=B0Lv=0.5×0.4×2V=0.4V,
由闭合电路欧姆定律,电路中的电流I=$\frac{E}{R+r}$=$\frac{0.4}{0.15+0.05}A=2A$
(2)由题意可知,在x=2m处,B2=B0+kx=1.5T,
切割产生感应电动势,E=B2Lv2,
由上可得,金属棒在x=2m处的速度v2=0.67m/s
(3)当x=0m时F0=B0IL=0.4N,
x=2m时,FA=B2IL=1.2N,
金属棒从x=0运动到x=2m过程中安培力做功的大小,W=( F0+FA)$\frac{x}{2}$=1.6J
(4)由EIt=W
解得t=2s,
由动能定理:$Pt-W=\frac{1}{2}mv_2^2-\frac{1}{2}mv_0^2$,
解得:P=0.71W
答:(1)电路中的电流2A;
(2)金属棒在x=2m处的速度0.67m/s;
(3)金属棒从x=0运动到x=2m过程中安培力做功的大小1.6J;
(4)金属棒从x=0运动到x=2m过程中外力的平均功率0.71W.
点评 本题考查法拉第电磁感应定律、闭合电路欧姆定律、安培力的大小公式、做功表达式、动能定理等的规律的应用与理解,运动过程中电阻上消耗的功率不变,是本题解题的突破口.

练习册系列答案
相关题目
17. 如图,甲图中理想变压器a、b两端加上220V的交流电压时,电压为110V;乙图中e、f两端加上220V的直流电压时,g、h间的电压为110V.现在c、d两端加上110V的交流电压,在g、h两端加上110V的直流电压,下列说法正确的是( )
如图,甲图中理想变压器a、b两端加上220V的交流电压时,电压为110V;乙图中e、f两端加上220V的直流电压时,g、h间的电压为110V.现在c、d两端加上110V的交流电压,在g、h两端加上110V的直流电压,下列说法正确的是( )
 如图,甲图中理想变压器a、b两端加上220V的交流电压时,电压为110V;乙图中e、f两端加上220V的直流电压时,g、h间的电压为110V.现在c、d两端加上110V的交流电压,在g、h两端加上110V的直流电压,下列说法正确的是( )
如图,甲图中理想变压器a、b两端加上220V的交流电压时,电压为110V;乙图中e、f两端加上220V的直流电压时,g、h间的电压为110V.现在c、d两端加上110V的交流电压,在g、h两端加上110V的直流电压,下列说法正确的是( )| A. | a、b两点间的电压为55V | |
| B. | e、f两点间的电压为220V | |
| C. | 若甲图中滑片往上移a、b两点间电压会减小 | |
| D. | 若乙图中滑片往上移e、f两点间电压会增加 |
7. 如图所示,悬线一端系一小球,另一端固定于O点,在O点正下方的P点钉一个钉子,使悬线拉紧与竖直方向成一角度θ然后由静止释放小球,当悬线碰到钉子时,下列说法正确的是( )
如图所示,悬线一端系一小球,另一端固定于O点,在O点正下方的P点钉一个钉子,使悬线拉紧与竖直方向成一角度θ然后由静止释放小球,当悬线碰到钉子时,下列说法正确的是( )
①小球的瞬时速度突然变大
②小球的加速度突然变大
③小球所需的向心力突然变大
④悬线所受的拉力突然变大.
 如图所示,悬线一端系一小球,另一端固定于O点,在O点正下方的P点钉一个钉子,使悬线拉紧与竖直方向成一角度θ然后由静止释放小球,当悬线碰到钉子时,下列说法正确的是( )
如图所示,悬线一端系一小球,另一端固定于O点,在O点正下方的P点钉一个钉子,使悬线拉紧与竖直方向成一角度θ然后由静止释放小球,当悬线碰到钉子时,下列说法正确的是( )①小球的瞬时速度突然变大
②小球的加速度突然变大
③小球所需的向心力突然变大
④悬线所受的拉力突然变大.
| A. | ①③④ | B. | ②③④ | C. | ①②④ | D. | ①②③ |
11. 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )
如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是( )| A. | 电荷从a到b加速度减小 | B. | b处电势能比a处电势能小 | ||
| C. | b处电势比a处电势高 | D. | 电荷在b处速度达到最小 |
12. 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
 如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )
如图所示,大小可以不计的带有同种电荷的小球A和B互相排斥,静止时两球位于同一水平面,绝缘细线与竖直方向的夹角分别为α和β,且α<β,由此可知( )| A. | A球的质量较大 | |
| B. | B球的质量较大 | |
| C. | B球受的拉力较大 | |
| D. | A球对B球的库仑力大于B球对A球的库仑力 |
 如图所示,在x轴下方存在着正交的匀强电场与匀强磁场,电场方向沿x轴正方向,电场强度的大小E1=20N/C,磁场方向垂直纸面向里,磁感应强度的大小B1=5T,一个质量为3g,电荷量q=2×10-3C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m,在x轴上方存在着正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方作匀速圆周运动,运动轨迹恰好与y轴相切,如图所示,试求:(g=10m/s2,sin37°=0.6,cos37°=0.8).
如图所示,在x轴下方存在着正交的匀强电场与匀强磁场,电场方向沿x轴正方向,电场强度的大小E1=20N/C,磁场方向垂直纸面向里,磁感应强度的大小B1=5T,一个质量为3g,电荷量q=2×10-3C的带正电小球自y轴上的M点沿直线匀速运动到x轴上的N点,且已知OM=4m,在x轴上方存在着正交的匀强电场E2与匀强磁场B2(图中均未画出),小球在x轴上方作匀速圆周运动,运动轨迹恰好与y轴相切,如图所示,试求:(g=10m/s2,sin37°=0.6,cos37°=0.8).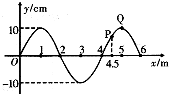 如图所示,是一列简谐横波在某一时刻的波形图象,已知该波沿x轴正方向传播,波速为5m/s,求:
如图所示,是一列简谐横波在某一时刻的波形图象,已知该波沿x轴正方向传播,波速为5m/s,求: 一质量为m=1.00kg的木块由静止沿固定光滑斜面滑下,斜面的倾角为θ=370,物体开始时离斜面底端的高度h=1.8m,(g=10m/s2)求:
一质量为m=1.00kg的木块由静止沿固定光滑斜面滑下,斜面的倾角为θ=370,物体开始时离斜面底端的高度h=1.8m,(g=10m/s2)求: