题目内容
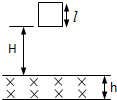 正方形的导线框,质量m=60g,边长l=12cm,电阻R=0.06Ω,在竖直平面内自由下落H=5m后,下框边进入水平方向的匀强磁场中,磁场方向与线框垂直,如图所示,匀强磁场沿竖直方向的宽度h=l,线框通过匀强磁场区域时恰好匀速直线运动,g=10m/s2,求:
正方形的导线框,质量m=60g,边长l=12cm,电阻R=0.06Ω,在竖直平面内自由下落H=5m后,下框边进入水平方向的匀强磁场中,磁场方向与线框垂直,如图所示,匀强磁场沿竖直方向的宽度h=l,线框通过匀强磁场区域时恰好匀速直线运动,g=10m/s2,求:(1)匀强磁场的磁感强度多大?
(2)线框通过磁场区域时产生了多少热量?
分析:(1)线框先做自由落体运动,由自由落体运动的速度位移公式可以求出线框进入磁场时的速度,线框在磁场中运动,受到安培力与重力作用,做匀速直线运动,由平衡条件可以求出磁感应强度大小.
(2)由速度公式的变形公式求出线框通过磁场的时间,由欧姆定律求出感应电流,最后由焦耳定律求出产生的焦耳热.
(2)由速度公式的变形公式求出线框通过磁场的时间,由欧姆定律求出感应电流,最后由焦耳定律求出产生的焦耳热.
解答:解:(1)线框做自由落体运动:v2=2gH,
框的下边进入磁场的速度为:v=
=
m/s=10m/s,
线框进入磁场时受到的安培力:F=BIl=Bl
=Bl
=
,
线框进入磁场后做匀速直线运动,处于平衡状态,由平衡条件得:
mg=
,
解得匀强磁场的磁感强度:
B=
=
T=0.5T;
(2)线框通过磁场区域的时间为:t=
=0.024s,
线框通过磁场时的感应电流:I=
,
由焦耳定律可知,全过程产生的热量:
Q=I2Rt=(
)2Rt=0.144J;
答:(1)匀强磁场的磁感强度0.5T.
(2)线框通过磁场区域时产生的热量为0.144J.
框的下边进入磁场的速度为:v=
| 2gH |
| 2×10×5 |
线框进入磁场时受到的安培力:F=BIl=Bl
| E |
| R |
| Blv |
| R |
| B2l2v |
| R |
线框进入磁场后做匀速直线运动,处于平衡状态,由平衡条件得:
mg=
| B2l2v |
| R |
解得匀强磁场的磁感强度:
B=
| 1 |
| l |
|
| 1 |
| 0.12 |
|
(2)线框通过磁场区域的时间为:t=
| 2l |
| v |
线框通过磁场时的感应电流:I=
| Blv |
| R |
由焦耳定律可知,全过程产生的热量:
Q=I2Rt=(
| Blv |
| R |
答:(1)匀强磁场的磁感强度0.5T.
(2)线框通过磁场区域时产生的热量为0.144J.
点评:本题考查了求磁感应强度、产生的焦耳热,应用E=BLv、欧姆定律、安培力公式、焦耳定律即可正确解题.

练习册系列答案
相关题目
 有一边长为L的正方形导线框,质量为m,由高度H处自由下落,如图所示,其下边ab进入匀强磁场区域后,线圈开始减速运动,直到其上边cd刚好穿出磁场时,速度减为ab边刚进入磁场时速度的一半,此匀强磁场的宽度也是L,线框在穿越匀强磁场过程中产生的电热是( )
有一边长为L的正方形导线框,质量为m,由高度H处自由下落,如图所示,其下边ab进入匀强磁场区域后,线圈开始减速运动,直到其上边cd刚好穿出磁场时,速度减为ab边刚进入磁场时速度的一半,此匀强磁场的宽度也是L,线框在穿越匀强磁场过程中产生的电热是( )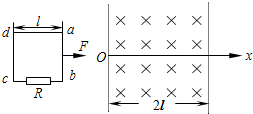 (2011?闸北区二模)如图所示abcd为一边长l、具有质量的正方形刚性导线框,位于水平面内,bc边中串接有电阻R,导线的电阻不计.虚线表示一匀强磁场区域的边界,它与线框的ab边平行,磁场区域的宽度为2l,磁感应强度为B,方向竖直向下.线框在一垂直于ab边的水平恒定拉力F作用下沿光滑水平面运动,直至通过磁场区域.已知ab边刚进入磁场时,线框便为匀速运动,此时通过R的电流大小为i0,则从导线框刚进入磁场到完全离开磁场的过程中,流过电阻R的电流i的大小随ab边的位置坐标x变化的图线可能是( )
(2011?闸北区二模)如图所示abcd为一边长l、具有质量的正方形刚性导线框,位于水平面内,bc边中串接有电阻R,导线的电阻不计.虚线表示一匀强磁场区域的边界,它与线框的ab边平行,磁场区域的宽度为2l,磁感应强度为B,方向竖直向下.线框在一垂直于ab边的水平恒定拉力F作用下沿光滑水平面运动,直至通过磁场区域.已知ab边刚进入磁场时,线框便为匀速运动,此时通过R的电流大小为i0,则从导线框刚进入磁场到完全离开磁场的过程中,流过电阻R的电流i的大小随ab边的位置坐标x变化的图线可能是( )
 (2008?岳阳二模)如图,有一边长为L的正方形导线框,质量为m,从距匀强磁场边界高度为H处自由下落,则下列对线圈进入磁场的过程中的运动性质描述可能正确的是( )
(2008?岳阳二模)如图,有一边长为L的正方形导线框,质量为m,从距匀强磁场边界高度为H处自由下落,则下列对线圈进入磁场的过程中的运动性质描述可能正确的是( )