题目内容
4.设地球的半径为R,表面重力加速度为g,则在围绕地球做匀速圆周运动的不同轨道的人造卫星中,(1)运行线速度的最大值是多大;
(2)周期的最小值是多少.
分析 设地球的质量为M,静止在地面上的物体质量为m,根据地球表面重力等于向心力列式,再根据人造地球卫星做匀速圆周运动时由万有引力提供向心力列式,由以上两式即可求得该人造地球卫星的线速度的最大值和最小周期.
解答 解:(1)根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
在地球表面重力与万有引力相等有:$\frac{GMm}{{{R}_{\;}}^{2}}$=mg
v=$\sqrt{\frac{GM}{r}}$,
当r=R时,运行线速度最大,
解得运行线速度的最大值vm=$\sqrt{gR}$,
(2)根据万有引力提供向心力得
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,
当r=R,人造地球卫星周期最小,
解得周期的最小值Tm=$2π\sqrt{\frac{{R}_{\;}}{g}}$,
答:(1)运行线速度的最大值是$\sqrt{gR}$;
(2)周期的最小值是$2π\sqrt{\frac{{R}_{\;}}{g}}$.
点评 本题是万有引力提供向心力公式和黄金代换的直接应用,难度不大,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
14.分子之间存在作用力,下列现象能够体现分子力的有( )
| A. | 铁丝很难被拉长,是分子间存在吸引力的宏观表现 | |
| B. | 水很难被压缩,是分子间存在斥力的宏观表现 | |
| C. | 气体总是很容易充满容器,是分子间存在斥力的宏观表现 | |
| D. | 磁铁可以吸引铁屑,是分子间存在吸引力的宏观表现 |
12.在排球比赛中如果运动员在近网处沿水平方向扣球.若把扣后排球的运动近似看作质点的平抛运动,则下列四种情况中,排球最有可能出界的是( )
| A. | 扣球点较低,扣出时排球的速度较大 | |
| B. | 扣球点较低,扣出时排球的速度较小 | |
| C. | 扣球点较高,扣出时排球的速度较大 | |
| D. | 扣球点较高,扣出时排球的速度较小 |
19.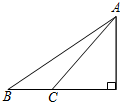 如图所示,一物体从斜面上端的A点分别沿动摩擦因数相同的粗糙面AB和AC滑到同一水平面上的B点和C点,下列说法正确的是( )
如图所示,一物体从斜面上端的A点分别沿动摩擦因数相同的粗糙面AB和AC滑到同一水平面上的B点和C点,下列说法正确的是( )
 如图所示,一物体从斜面上端的A点分别沿动摩擦因数相同的粗糙面AB和AC滑到同一水平面上的B点和C点,下列说法正确的是( )
如图所示,一物体从斜面上端的A点分别沿动摩擦因数相同的粗糙面AB和AC滑到同一水平面上的B点和C点,下列说法正确的是( )| A. | 沿AB面重力做的功多 | B. | 沿AC面重力做的功多 | ||
| C. | 沿AC面物体克服摩擦力做的功多 | D. | 沿AB面物体克服摩擦力做的功多 |
9. 2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
 2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )
2004年8月12日下午,上海某中心广场行人拥挤,突然有人高喊“楼要倒了!”其他人猛然抬头向上看感觉楼在慢慢倾倒,如图所示.于是大家便纷纷狂奔逃生,结果引起了交通混乱.但过了好久,高楼并没有倒塌,人们再仔细观察时,高楼依然稳稳地矗立在那里.关于人们感觉楼要倾倒的原因,下列说法正确的是( )| A. | 楼在倾倒 | B. | 人在运动 | ||
| C. | 选择了旁边更高的楼为参考系 | D. | 选择了高空运动的云为参考系 |
10.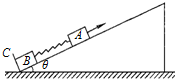 在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
 在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )
在倾角为θ的光滑固定斜面上有两个用轻弹簧连接的物块A和B,它们的质量分别为m和2m,弹簧的劲度系数为k,C为一固定挡板,系统处于静止状态.现用一沿斜面方向的恒力拉物块A使之沿斜面向上运动,当B刚离开C时,A的速度为v,加速度为a,且方向沿斜面向上.设弹簧始终处于弹性限度内,重力加速度为g,则( )| A. | 当B刚离开C时,A发生的位移大小为$\frac{3mgsinθ}{k}$ | |
| B. | 从静止到B刚离开C的过程中,物块A克服重力做功为$\frac{3{m}^{2}{g}^{2}sinθ}{k}$ | |
| C. | B刚离开C时,恒力对A做功的功率为(2mgsinθ+ma)v | |
| D. | 当A的速度达到最大时,B的加速度大小为$\frac{a}{2}$ |
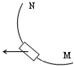
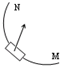
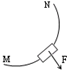
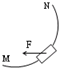
 如图所示,水平放置的绝对绝缘桌面上有一个金属圆环,圆心的正上方有一个竖直的条形磁铁,当条形磁铁水平向右移动时,金属圆环受到驱动力的方向是( )
如图所示,水平放置的绝对绝缘桌面上有一个金属圆环,圆心的正上方有一个竖直的条形磁铁,当条形磁铁水平向右移动时,金属圆环受到驱动力的方向是( )