题目内容
B(选修模块 3 一4)
( l )一个摆长为 L 的单摆做简谐运动,若从某时刻开始计时(取t=0),当 t=
时,摆球具有负向最大加速度,则单摆的位移 x 随时间 t 变化的图象(如图1)是 .

( 2 )如图2所示为一列简谐波在 tl=0 时刻的图象,此时波中质点 M 的运动方向沿y轴正方向,到 t2=0.65s 时质点 M 恰好第 4 次到达y轴正方向最大位移处,则该波的传播方向为 ,波速为 m/s.
( 3 )一组平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图3所示.已知光线 I 沿直线穿过玻璃,它的入射点是O,光线Ⅱ的入射点为 A,穿过玻璃后两条光线交于一点.已知玻璃截面的圆半径为 R,0A=
,玻璃的折射率n=
.求两条光线射出玻璃后的交点与O点的距离.
( l )一个摆长为 L 的单摆做简谐运动,若从某时刻开始计时(取t=0),当 t=
| 3π |
| 2 |
|

( 2 )如图2所示为一列简谐波在 tl=0 时刻的图象,此时波中质点 M 的运动方向沿y轴正方向,到 t2=0.65s 时质点 M 恰好第 4 次到达y轴正方向最大位移处,则该波的传播方向为
( 3 )一组平行的细激光束,垂直于半圆柱玻璃的平面射到半圆柱玻璃上,如图3所示.已知光线 I 沿直线穿过玻璃,它的入射点是O,光线Ⅱ的入射点为 A,穿过玻璃后两条光线交于一点.已知玻璃截面的圆半径为 R,0A=
| R |
| 2 |
| 3 |
分析:(1)根据单摆的周期公式知,t=
时,经历了
T,摆球具有负向的最大加速度,知处于正向最大位移处,根据该规律确定单摆的位移时间图线.
(2)根据质点的振动方向,通过上下坡法确定波的传播方向.根据质点 M 恰好第 4 次到达y轴正方向最大位移处,求出质点的周期,通过波长求出波速的大小.
(3)作出光路图,结合折射定律和几何关系求出两条光线射出玻璃后的交点与O点的距离.
| 3π |
| 2 |
|
| 3 |
| 4 |
(2)根据质点的振动方向,通过上下坡法确定波的传播方向.根据质点 M 恰好第 4 次到达y轴正方向最大位移处,求出质点的周期,通过波长求出波速的大小.
(3)作出光路图,结合折射定律和几何关系求出两条光线射出玻璃后的交点与O点的距离.
解答:解:(1)单摆的周期T=2π
,t=
时,经历了
T,摆球具有负向的最大加速度,知处于正向最大位移处,可知零时刻处于平衡位置,且向负方向运动,故B正确,A、C、D错误.
故选B.
(2)波中质点 M 的运动方向沿y轴正方向,根据上下坡法,知波的传播方向为+x方向.到 t2=0.65s 时质点 M 恰好第 4 次到达y轴正方向最大位移处,因为经过
T第一次到达y轴正向最大位移处,则有3
T=0.65s,解得T=0.2s.则波速v=
=
m/s=2m/s.
(3)两条光线的光路图如图所示,设射出玻璃后的交点是P,光线Ⅱ从玻璃射出时的入射角为i,折射角为r,根据折射定律得,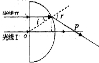
n=
由几何关系可得i=30°
代入r=60°
由几何关系可得:OP=2Rcos30°=
R.
故答案为:(1)B (2)+x方向,2m/s (3)
R
|
| 3π |
| 2 |
|
| 3 |
| 4 |
故选B.
(2)波中质点 M 的运动方向沿y轴正方向,根据上下坡法,知波的传播方向为+x方向.到 t2=0.65s 时质点 M 恰好第 4 次到达y轴正方向最大位移处,因为经过
| 1 |
| 4 |
| 1 |
| 4 |
| λ |
| T |
| 0.4 |
| 0.2 |
(3)两条光线的光路图如图所示,设射出玻璃后的交点是P,光线Ⅱ从玻璃射出时的入射角为i,折射角为r,根据折射定律得,

n=
| sinr |
| sini |
由几何关系可得i=30°
代入r=60°
由几何关系可得:OP=2Rcos30°=
| 3 |
故答案为:(1)B (2)+x方向,2m/s (3)
| 3 |
点评:本题考查了振动和波动的关系以及几何光学问题,难度不大,关键要熟悉教材,理解基本规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 C.(选修模块 3 一 5 )
C.(选修模块 3 一 5 )  C.(选修模块 3 一 5 )
C.(选修模块 3 一 5 ) 
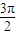
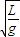 时,摆球具有负向最大加速度,则单摆的位移 x 随时间 t 变化的图象(如图1)是______.
时,摆球具有负向最大加速度,则单摆的位移 x 随时间 t 变化的图象(如图1)是______.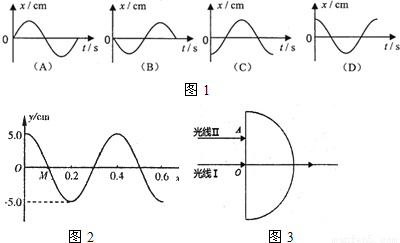
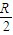 ,玻璃的折射率n=
,玻璃的折射率n=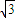 .求两条光线射出玻璃后的交点与O点的距离.
.求两条光线射出玻璃后的交点与O点的距离.