题目内容
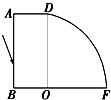 如图所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为
如图所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为| 1 | 4 |
(1)画出光路图;
(2)求该棱镜的折射率n和光线在棱镜中传播的速度大小v(光在真空中的传播速度c=3.0×108m/s).
分析:(1)光线射入棱镜后射在BF面上的O点并恰好不从BF面射出,在BF面上发生全反射.作出光路图.
(2)根据折射定律分别研究光线在AB面上的折射和在BF面的全反射,求解折射率.
(2)根据折射定律分别研究光线在AB面上的折射和在BF面的全反射,求解折射率.
解答: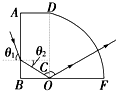 解:(1)光路图如图所示.
解:(1)光路图如图所示.
(2)设光线在AB面的折射角为θ2,折射光线与OD的夹角为C,则由题意,光线在BF面恰好发生全反射,则sinC=
由几何知识可知,θ2+C=90°,得:
sinθ2=cosC=
=
由折射定律得:n=
联立得:sin60°=nsinθ2=
解得 n≈1.3
故 v=
=
m/s≈2.3×108m/s
答:
(1)画出光路图如图所示;
(2)该棱镜的折射率n为1.3,光线在棱镜中传播的速度大小v是2.3×108m/s.
 解:(1)光路图如图所示.
解:(1)光路图如图所示. (2)设光线在AB面的折射角为θ2,折射光线与OD的夹角为C,则由题意,光线在BF面恰好发生全反射,则sinC=
| 1 |
| n |
由几何知识可知,θ2+C=90°,得:
sinθ2=cosC=
| 1-sin2C |
1-
|
由折射定律得:n=
| sinθ1 |
| sinθ2 |
联立得:sin60°=nsinθ2=
| n2-1 |
解得 n≈1.3
故 v=
| c |
| n |
| 3×108 |
| 1.3 |
答:
(1)画出光路图如图所示;
(2)该棱镜的折射率n为1.3,光线在棱镜中传播的速度大小v是2.3×108m/s.
点评:本题是折射现象和全反射现象的综合,首先要正确作出光路图,运用几何知识和折射定律求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012?武昌区模拟)如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角θ1=45°,它进入棱镜后恰好以临界角射在BC面上的O点.
(2012?武昌区模拟)如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD为半径为R的四分之一的圆周,圆心为O,光线从AB面上的某点入射,入射角θ1=45°,它进入棱镜后恰好以临界角射在BC面上的O点.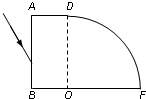 如图所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为
如图所示为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为 如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD是半径为R的四分之一圆周,圆心为O,光线从AB面上的某点入射,入射角i=45°,光进入棱镜后恰好在BC面上的O点发生全反射,后由CD面射出.
如图所示为用某种透明材料制成的一块柱形棱镜的截面图,圆弧CD是半径为R的四分之一圆周,圆心为O,光线从AB面上的某点入射,入射角i=45°,光进入棱镜后恰好在BC面上的O点发生全反射,后由CD面射出.