题目内容
18. 如图所示为半径R=0.40m的四分之一竖直圆弧轨道,OA在水平方向,底端距水平地面的高度h=0.45m.一质量m=2.0kg的小滑块从圆弧轨道顶端A由静止释放,到达轨道底端B点的速度v=2.0m/s.忽略空气的阻力.取g=10m/s2.求:
如图所示为半径R=0.40m的四分之一竖直圆弧轨道,OA在水平方向,底端距水平地面的高度h=0.45m.一质量m=2.0kg的小滑块从圆弧轨道顶端A由静止释放,到达轨道底端B点的速度v=2.0m/s.忽略空气的阻力.取g=10m/s2.求:(1)小滑块从A点运动到B点的过程中,摩擦力所做的功W;
(2)小滑块在圆弧轨道底端B点受到的支持力大小FN;
(3)小滑块落地点与B点的水平距离x.
分析 (1)根据小滑块在B点对轨道的压力求得滑块的速度,根据动能定理求得滑块从A到B过程中克服摩擦力做的功;
(2)在B点由向心力公式可求得支持力的大小;
(3)小滑块离开B点后做平抛运动,根据平知识求得落地点C距轨道最低点B的水平距离.
解答 解:(1)小滑块由A到B的过程中,根据动能定理得:mgR+W=$\frac{1}{2}$mv2-0,
代入数据解得:W=-4J;
(2)在B点,根据牛顿第二定律有:FN-mg=m$\frac{{v}^{2}}{R}$
代入数据解得:FN=40N
(3)小滑块从B点出发做平抛运动,根据平抛运动的规律得:
水平方向:x=vt
竖直方向:h=$\frac{1}{2}$gt2,
代入数据解得:x=0.6m;
答:(1)小滑块由A到B的过程中,摩擦力所做的功W为-4J;
(2)小滑块在圆弧轨道底端B点受到的支持力大小为40N;
(3)小滑块落地点与B点的水平距离x为0.6m
点评 能根据牛顿第二定律公式由作用力求出滑块运动的速度,由动能定理和平抛知识求解,关键是小滑块在B点时合外力提供向心力,不是轨道对滑块的支持力直接提供向心力.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
8. 用细线将篮球拴在升降机光滑的侧壁上,当升降机加速下降时,出现如图所示的情形.四位同学对此现象做出了分析与判断,其中可能正确的是( )
用细线将篮球拴在升降机光滑的侧壁上,当升降机加速下降时,出现如图所示的情形.四位同学对此现象做出了分析与判断,其中可能正确的是( )
 用细线将篮球拴在升降机光滑的侧壁上,当升降机加速下降时,出现如图所示的情形.四位同学对此现象做出了分析与判断,其中可能正确的是( )
用细线将篮球拴在升降机光滑的侧壁上,当升降机加速下降时,出现如图所示的情形.四位同学对此现象做出了分析与判断,其中可能正确的是( )| A. | 升降机的加速度大于g,侧壁对球无挤压 | |
| B. | 升降机的加速度小于g,侧壁对球有挤压 | |
| C. | 升降机的加速度等于g,侧壁对球无挤压 | |
| D. | 升降机的加速度等于g,侧壁对球有挤压 |
9.关于传感器,下列说法正确的是( )
| A. | 电子秤中的应变片是力的传感器 | |
| B. | 火灾报警器通常是将光信号转变为电信号 | |
| C. | 干簧管是一种能够感知温度的传感器 | |
| D. | 霍尔元件是磁敏器件,可以利用它测量电流的大小 |
6.物体做曲线运动时,下列说法中正确的是( )
| A. | 速度大小一定是变化的 | B. | 速度方向一定是变化的 | ||
| C. | 合力一定是变化的 | D. | 加速度一定是变化的 |
3.下列说法正确的是( )
| A. | 做曲线运动物体的速度和加速度时刻都在变化 | |
| B. | 卡文迪许通过扭秤实验得出了万有引力定律 | |
| C. | 1847年德国物理学家亥姆霍兹在理论上概括和总结了自然界中最重要、最普遍的规律之一能量守恒定律 | |
| D. | 一对作用力与反作用力做的总功一定为0 |
7. 轻质弹簧吊着小球静止在如图所示的A位置,现用水平外力F将小球缓慢拉到B位置,此时弹簧与竖直方向的夹角为θ,在这一过程中,下列说法正确的是( )
轻质弹簧吊着小球静止在如图所示的A位置,现用水平外力F将小球缓慢拉到B位置,此时弹簧与竖直方向的夹角为θ,在这一过程中,下列说法正确的是( )
 轻质弹簧吊着小球静止在如图所示的A位置,现用水平外力F将小球缓慢拉到B位置,此时弹簧与竖直方向的夹角为θ,在这一过程中,下列说法正确的是( )
轻质弹簧吊着小球静止在如图所示的A位置,现用水平外力F将小球缓慢拉到B位置,此时弹簧与竖直方向的夹角为θ,在这一过程中,下列说法正确的是( )| A. | 小球的弹性势能不变,重力势能增加 | |
| B. | 弹簧对小球的弹力在水平方向的分力大小逐渐增大 | |
| C. | 水平外力F做的功数值上等于弹簧和小球机械能的增加量 | |
| D. | 水平外力F做的功等于弹簧的弹性势能增加 |
8. 一人乘电梯从1楼到30楼,经历了先加速、后匀速、再减速的运动过程,则人受到的支持力对人做功情况是( )
一人乘电梯从1楼到30楼,经历了先加速、后匀速、再减速的运动过程,则人受到的支持力对人做功情况是( )
 一人乘电梯从1楼到30楼,经历了先加速、后匀速、再减速的运动过程,则人受到的支持力对人做功情况是( )
一人乘电梯从1楼到30楼,经历了先加速、后匀速、再减速的运动过程,则人受到的支持力对人做功情况是( )| A. | 加速时做正功,匀速时不做功,减速时做负功 | |
| B. | 加速时做正功,匀速和减速时做负功 | |
| C. | 加速和匀速时做正功,减速时做负功 | |
| D. | 始终做正功 |
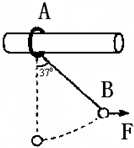 如图所示,在水平粗糙横杆上,有一质量为m的小圆环A,用一细线悬吊一个质量为m的球B.现用一水平拉力缓慢地拉起球B,使细线与竖直方向成37°角,此时环A仍保持静止.求:
如图所示,在水平粗糙横杆上,有一质量为m的小圆环A,用一细线悬吊一个质量为m的球B.现用一水平拉力缓慢地拉起球B,使细线与竖直方向成37°角,此时环A仍保持静止.求: