题目内容
如图所示，一薄木板斜搁在高度一定的平台和水平地板上，其顶端与平台相平，末端置于地板的P处，并与地板平滑连接。将一可看成质点的滑块自木板顶端无初速释放，沿木板下滑，接着在地板上滑动，最终停在Q处。滑块和木板及地板之间的动摩擦因数相同。现将木板截短一半，仍按上述方式搁在该平台和水平地板上，再次将滑块自木板顶端无初速释放，（设物体在板和地面接触处平滑过渡），则滑块最终将停在
| A．P处 | B．P、Q之间 | C．Q处 | D．Q的右侧 |
C
试题分析：假设斜面与水平面的夹角为α，斜面的高度为h，斜面在水平方向的投影为
在斜面上克服摩擦力做的功
①设在水平面上滑行的距离为
怎在水平面上克服摩擦力做的功
整个过程克服摩擦力做得功为
②由此公式可知，摩擦力做得功与斜面的夹角无关，
又由于从相同的高度滑下，根据动能定理得：
③②③联立可知，
最终还是停在Q处，故ABD错，C正确；
故选C．
点评：解决本题的关键是掌握摩擦力做功的特点的理解及力对物体做功的公式的灵活运用．
练习册系列答案
相关题目
，劲度系数
的轻质光滑弹簧平行于传送带放置，下端固定在水平地面上，另一端自由状态时位于Q点。小滑块质量
，放置于传送带P点，滑块与传送带间的滑动摩擦因数
。 已知传送带足够长，最大静摩擦力可认为和滑动摩擦力相等， 整个过程中小滑块未脱离传送带，弹簧处于弹性限度内，弹簧的弹性势能
，x为弹簧的形变量 (重力加速度g=10m/s2,sin370=0.6,cos370=0.8）
，求小物块滑行的最大距离
；
速度逆时针传动，将小滑块无初速放在P点， PQ距离
，求小物块滑行的最大距离
。
的速度匀速运转，现将一质量为
的小物体（可视为质点）轻放在传送带上A点，已知小物体从A到B的时间一共为8s，则在传送带将小物块从A传送到B的过程中，求：
轻放一个同样的物体，当物体稳定运行时，相邻匀速运动的两物体之间的距离为多大？
）
和
，下滑过程中克服摩擦力所做功分别为
和
，则（ ）
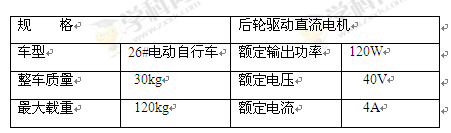
速度。