题目内容
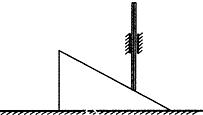 如图所示,光滑金属直杆穿过竖直固定的滑套,其底端置于光滑斜面体上,金属杆质量为m1,斜面体质量为m2,现给斜面体一水平推力使斜面体从静止开始向右作匀加速直线运动,经t时间斜面体水平移动s,该过程中斜面体未碰到滑套,金属杆匀加速上升h高度重力加速度为g,求:
如图所示,光滑金属直杆穿过竖直固定的滑套,其底端置于光滑斜面体上,金属杆质量为m1,斜面体质量为m2,现给斜面体一水平推力使斜面体从静止开始向右作匀加速直线运动,经t时间斜面体水平移动s,该过程中斜面体未碰到滑套,金属杆匀加速上升h高度重力加速度为g,求:(1)该过程中金属杆受到的合外力;
(2)该过程中水平推力的平均功率.
分析:(1)由金属杆匀加速上升高度,可得其加速度,由牛顿第二定律可得合外力;
(2)由运动学可表示金属杆和斜面体的末速度,由能量的转化和守恒可知:外力做的功转化为金属杆的动能和重力势能,以及斜面体的动能.
(2)由运动学可表示金属杆和斜面体的末速度,由能量的转化和守恒可知:外力做的功转化为金属杆的动能和重力势能,以及斜面体的动能.
解答:解:(1)设金属杆匀加速运动的加速度为a1,在该过程中有:
h=
a1t2…①
设金属杆受到的合外力为F,由牛顿第二定律得:
F=m1a1…②
由①②式可得:F=
.
金属杆合力方向与加速度方向一致,方向竖直向上.
(2)设该过程末金属杆和斜面体的速度分别为v1、v2,加速过程中斜面体的加速度为a2,由运动学方程有:v1=a1t,v2=a2t…③
s=
a2t2…④
设该过程中外力的平均功率为P,对金属杆和斜面体组成的系统,由功能关系得:
Pt=
m1v12+
m2v22+m1gh…⑤
由①式和③~⑤式可得:P=
.
答:(1)该过程中金属杆受到的合外力F=
;
(2)该过程中水平推力的平均功率P=
.
h=
| 1 |
| 2 |
设金属杆受到的合外力为F,由牛顿第二定律得:
F=m1a1…②
由①②式可得:F=
| 2m1h |
| t2 |
金属杆合力方向与加速度方向一致,方向竖直向上.
(2)设该过程末金属杆和斜面体的速度分别为v1、v2,加速过程中斜面体的加速度为a2,由运动学方程有:v1=a1t,v2=a2t…③
s=
| 1 |
| 2 |
设该过程中外力的平均功率为P,对金属杆和斜面体组成的系统,由功能关系得:
Pt=
| 1 |
| 2 |
| 1 |
| 2 |
由①式和③~⑤式可得:P=
| 2(m1h2+m2s2)+m1ght2 |
| t3 |
答:(1)该过程中金属杆受到的合外力F=
| 2m1h |
| t2 |
(2)该过程中水平推力的平均功率P=
| 2(m1h2+m2s2)+m1ght2 |
| t3 |
点评:本题关键是掌握好系统能量转化和守恒的应用,这个要综合考虑好各个物体的能量变化,比单个物体的能量转化和守恒难很多.

练习册系列答案
相关题目
 如图所示,光滑金属直轨道MN和PQ固定在同一水平面内,MN、PQ平行且足够长,两轨道间的宽度L=0.50m.轨道左端接一阻值R=0.50Ω的电阻.轨道处于磁感应强度大小B=0.40T,方向竖直向下的匀强磁场中.质量m=0.50kg的导体棒ab垂直于轨道放置.在沿着轨道方向向右的力F作用下,导体棒由静止开始运动,导体棒与轨道始终接触良好并且相互垂直.不计轨道和导体棒的电阻,不计空气阻力.
如图所示,光滑金属直轨道MN和PQ固定在同一水平面内,MN、PQ平行且足够长,两轨道间的宽度L=0.50m.轨道左端接一阻值R=0.50Ω的电阻.轨道处于磁感应强度大小B=0.40T,方向竖直向下的匀强磁场中.质量m=0.50kg的导体棒ab垂直于轨道放置.在沿着轨道方向向右的力F作用下,导体棒由静止开始运动,导体棒与轨道始终接触良好并且相互垂直.不计轨道和导体棒的电阻,不计空气阻力.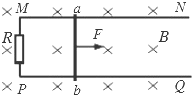 如图所示,光滑金属直轨道MN和PQ固定在同一水平面内,MN、PQ平行且足够长,两轨道间的宽度L=0.50m.平行轨道左端接一阻值R=0.50Ω的电阻.轨道处于磁感应强度大小B=0.40T,方向垂直导轨平面向下的匀强磁场中.一导体棒ab垂直于轨道放置.导体棒在垂直导体棒且水平向右的外力F作用下向右匀速运动,速度大小v=5.0m/s,导体棒与轨道始终接触良好并且相互垂直.不计轨道和导体棒的电阻,不计空气阻力.求
如图所示,光滑金属直轨道MN和PQ固定在同一水平面内,MN、PQ平行且足够长,两轨道间的宽度L=0.50m.平行轨道左端接一阻值R=0.50Ω的电阻.轨道处于磁感应强度大小B=0.40T,方向垂直导轨平面向下的匀强磁场中.一导体棒ab垂直于轨道放置.导体棒在垂直导体棒且水平向右的外力F作用下向右匀速运动,速度大小v=5.0m/s,导体棒与轨道始终接触良好并且相互垂直.不计轨道和导体棒的电阻,不计空气阻力.求