题目内容
8. 长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动,现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为$\sqrt{6gL}$,则小球在C点( )
长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动,现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为$\sqrt{6gL}$,则小球在C点( )| A. | 速度等于$\sqrt{gL}$ | B. | 速度小于$\sqrt{gL}$ | ||
| C. | 受到轻杆向上的弹力 | D. | 受到轻杆向下的弹力 |
分析 根据动能定理求出小球在C点的速度,结合牛顿第二定律求出轻杆对小球的弹力方向.
解答 解:A、根据动能定理得:$-mg•2L=\frac{1}{2}m{{v}_{C}}^{2}-\frac{1}{2}m{{v}_{D}}^{2}$,
解得:${v}_{C}=\sqrt{2gL}$,故A、B错误.
C、根据牛顿第二定律得:F+mg=m$\frac{{{v}_{C}}^{2}}{L}$,解得:F=mg,杆对小球的弹力方向向下,故C错误,D正确.
故选:D.
点评 本题考查了动能定理和牛顿第二定律的基本运用,知道最高点向心力的来源,知道杆子可以表现为拉力,也可以表现为支持力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.为了研究轻质弹簧的弹性势能与弹簧压缩量的关系,某实验小组的实验装置如图1所示,光滑水平桌面距地面高为h,一轻质弹簧左端固定,右端与质量为m的小钢球接触,弹簧处于原长.将小球向左推,压缩弹簧一段距离后由静止释放,弹簧将小球沿水平方向推出,小球落到位于水平地面的记录纸上,留下痕迹,已知重力加速度为g
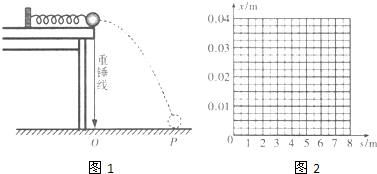
(1)某次实验测得小球的落点P到O点的距离为S,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$;
(2)改变弹簧压缩量进行多次实验,测量数据如表所示,请在图2坐标纸上做出x-s图象.
(3)由图象得出x与s的关系式为x=0.005s;由实验得到弹簧弹性势能Ep与弹簧压缩量x之间的关系式为Ep=$\frac{{{10}^{4}mgx}^{2}}{h}$.

(1)某次实验测得小球的落点P到O点的距离为S,那么由理论分析得到小球释放前压缩弹簧的弹性势能Ep与h、s、mg之间的关系式为Ep=$\frac{m{gs}^{2}}{4h}$;
(2)改变弹簧压缩量进行多次实验,测量数据如表所示,请在图2坐标纸上做出x-s图象.
| 弹簧压缩量x/m | 0.010 | 0.015 | 0.020 | 0.025 | 0.030 | 0.035 |
| 小球飞行水平距离s/m | 2.0 | 3.0 | 4.1 | 5.9 | 6.0 | 7.0 |
16.质量为200g,初速度为0的小球,被以10m/s的速度与水平方向成60°角抛出,则人对小球做的功为( )
| A. | 10J | B. | 5J | C. | 20J | D. | 10$\sqrt{3}$J |
3. 如图所示,为负点电荷电场中的一条电场线.A、B是该电场线上的两点,EA和EB分别表示A、B两点电场强度的大小.则下面说法中正确的是( )
如图所示,为负点电荷电场中的一条电场线.A、B是该电场线上的两点,EA和EB分别表示A、B两点电场强度的大小.则下面说法中正确的是( )
 如图所示,为负点电荷电场中的一条电场线.A、B是该电场线上的两点,EA和EB分别表示A、B两点电场强度的大小.则下面说法中正确的是( )
如图所示,为负点电荷电场中的一条电场线.A、B是该电场线上的两点,EA和EB分别表示A、B两点电场强度的大小.则下面说法中正确的是( )| A. | EA>EB | |
| B. | EA=EB | |
| C. | EA<EB | |
| D. | 因不知周围电场线的分布,故无法判断 |
13.下列说法中正确的是( )
| A. | 布朗运动是分子的热运动 | |
| B. | 液体表面产生张力的原因是液体表面层的分子较稀疏,分子间的引力大于斥力 | |
| C. | 做功和热传递都是通过能量转化的方式改变系统内能的 | |
| D. | 根据热力学定律,任何热机的效率都不会达到100% | |
| E. | 一定质量的理想气体,当它的压强、体积都增大时,其内能一定增加 |
17. 图示为某测速装置测出的某物体做直线运动的速度-时间图象,已知初速度为v0,末速度为v,则t时间内,物体通过的位移( )
图示为某测速装置测出的某物体做直线运动的速度-时间图象,已知初速度为v0,末速度为v,则t时间内,物体通过的位移( )
 图示为某测速装置测出的某物体做直线运动的速度-时间图象,已知初速度为v0,末速度为v,则t时间内,物体通过的位移( )
图示为某测速装置测出的某物体做直线运动的速度-时间图象,已知初速度为v0,末速度为v,则t时间内,物体通过的位移( )| A. | 大于$\frac{{{v_0}+{v_{\;}}}}{2}$t | B. | 等于$\frac{{{v_0}+{v_{\;}}}}{2}$t | ||
| C. | 小于$\frac{{{v_0}+{v_{\;}}}}{2}$t | D. | 以上答案都有可能的 |
18.如图所示,带电粒子在电场中由A点移到B点,可判知( )


| A. | 粒子带负电 | |
| B. | 粒子的电势能不断增加 | |
| C. | 粒子的动能不断减少 | |
| D. | 粒子在B点的加速度大于在A点的加速度 |
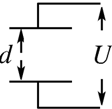 如图所示,一平行板电容器接在U=12V的直流电源上,电容C=3.0×10-10F,两极板间距离d=1.20×10-3m,取g=10m/s2,求:
如图所示,一平行板电容器接在U=12V的直流电源上,电容C=3.0×10-10F,两极板间距离d=1.20×10-3m,取g=10m/s2,求: