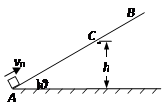题目内容
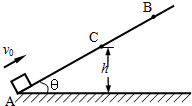 如图,让一小物体(可看作质点)从图示斜面上的A点以v0=4m/s的初速度滑上斜面,物体滑到斜面上的B点后沿原路返回.若A到B的距离为1m,斜面倾角为θ=37°.(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图,让一小物体(可看作质点)从图示斜面上的A点以v0=4m/s的初速度滑上斜面,物体滑到斜面上的B点后沿原路返回.若A到B的距离为1m,斜面倾角为θ=37°.(sin37°=0.6,cos37°=0.8,g=10m/s2)(1)求物体与斜面间的动摩擦因数;
(2)若设水平地面为零重力势能面,且物体返回经过C点时,其动能恰与重力势能相等,求C点相对水平地面的高度h.
分析:(1)题既可以用动能定理求解也可以用牛顿运动定律求解,但用动能定理更简洁.(2)题从B到C利用动能定理再结合动能等于重力势能即可求解.
解答:解:(1)设物体与斜面间的滑动摩擦因数为μ,则物体上滑由A到B做速度由v0变为0的匀减速运动,由动能定理有
-mgssinθ-μmgscosθ=0-
,代入数据解得μ=0.25
(本题也可用牛顿运动定律求解:由牛顿第二定律有mgsinθ+μmgcosθ=ma…①,
又由运动学公式,可得0-v02=-2a?AB…②,
由①②联立,代入数据可得μ=0.25)
即物体与斜面间的动摩擦因数为0.25.
(2)设物体返回经过C点时速度大小为v1,则对于物体由B到C,
由动能定理有mg(ABsinθ-h)-μmgcosθ.
=
m
又
m
=mgh,
联立以上两式解得h=
AB
代入数据可得:h=0.24m
即动能与势能相等时C点相对地面的高度为0.24m.
-mgssinθ-μmgscosθ=0-
| 1 |
| 2 |
| mv | 2 |
(本题也可用牛顿运动定律求解:由牛顿第二定律有mgsinθ+μmgcosθ=ma…①,
又由运动学公式,可得0-v02=-2a?AB…②,
由①②联立,代入数据可得μ=0.25)
即物体与斜面间的动摩擦因数为0.25.
(2)设物体返回经过C点时速度大小为v1,则对于物体由B到C,
由动能定理有mg(ABsinθ-h)-μmgcosθ.
| AB.sinθ-h |
| sinθ |
| 1 |
| 2 |
| v | 2 |
又
| 1 |
| 2 |
| v | 2 |
联立以上两式解得h=
| sinθ-μcosθ |
| 2-μcosθ |
代入数据可得:h=0.24m
即动能与势能相等时C点相对地面的高度为0.24m.
点评:在涉及到“功”、“动能”字眼、速度大小、位移大小,不管是恒力还是变力,直线运动还是曲线运动,要首选动能定理解决.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目