题目内容
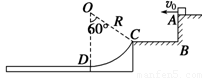
质量为m=(1)小物块离开A点的水平初速度v1;
(2)小物块经过O点时对轨道的压力;
(3)斜面上CD间的距离;
(4)假设小物块与传送带间的动摩擦因数为μ2=0.3,传送带的速度为

解:(1)对小物块,由A到B有
vy2=2gh
在B点tan![]() =
=![]()
所以v1=
(2)对小物块,由B到O有
mgR(1-sin37°)=![]() mv02-
mv02-![]() mvb2其中vb=
mvb2其中vb=![]() m/s=
m/s=
在O点N-mg=m![]()
所以N=43 N
由牛顿第三定律知对轨道的压力为N′=43 N
(3)物块沿斜面上滑:mgsin53°+μ1mgcos53°=ma1
所以a1=
物块沿斜面上滑:mgsin53°-μ1mgcos53°=ma2
由机械能守恒知vc=vb=
小物块由C上升到最高点历时t1=![]() =0.5 s
=0.5 s
小物块由最高点回到D点历时t2=0.8 s-0.5 s=0.3 s
故SCD=![]() t1-
t1-![]() a2t22
a2t22
即SCD=0.98 m
(4)小物块在传送带上加速过程:μ2mg=ma3
PA间的距离是SPA=![]() =1.5 m
=1.5 m

练习册系列答案
相关题目