题目内容
3.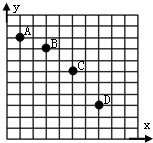 如图所示,A、B、C、D是某小球做平抛运动过程中经过竖直平面内的方格纸上的不同位置,已知方格纸上每一小格的边长为L,当地重力加速度为g,则小球做平抛运动的初速度大小为v0=$2\sqrt{gL}$,小球经过C点的速度大小为vc=$\frac{1}{2}\sqrt{41gL}$.
如图所示,A、B、C、D是某小球做平抛运动过程中经过竖直平面内的方格纸上的不同位置,已知方格纸上每一小格的边长为L,当地重力加速度为g,则小球做平抛运动的初速度大小为v0=$2\sqrt{gL}$,小球经过C点的速度大小为vc=$\frac{1}{2}\sqrt{41gL}$.
分析 在竖直方向上根据连续相等时间内的位移之差是一恒量求出相等的时间间隔,结合水平位移和时间间隔求出初速度大小,根据某段时间内的平均速度等于中间时刻的瞬时速度求出C点的竖直分速度,结合平行四边形定则求出C点的速度.
解答 解:在竖直方向上,根据△y=L=gT2得,T=$\sqrt{\frac{L}{g}}$,
则初速度${v}_{0}=\frac{2L}{T}=\frac{2L}{\sqrt{\frac{L}{g}}}=2\sqrt{gL}$.
C点的竖直分速度${v}_{cy}=\frac{5L}{2T}$=$\frac{5\sqrt{gL}}{2}$,
根据平行四边形定则知,C点的速度${v}_{C}=\sqrt{{{v}_{0}}^{2}+{{v}_{cy}}^{2}}$=$\sqrt{4gL+\frac{25gL}{4}}$=$\frac{1}{2}\sqrt{41gL}$.
故答案为:$2\sqrt{gL}$,$\frac{1}{2}\sqrt{41gL}$.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解,难度中等.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
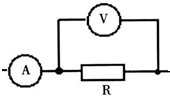
18.如图所示的电路测量待测电阻RX的阻值时,下列关于测量误差的说法中正确的是( )

| A. | 实验误差主要来源于电压测量不准确 | |
| B. | 电流表的示数等于通过电阻的电流 | |
| C. | 这个电路图适合测量电阻值较大的电阻值 | |
| D. | 实验测得电阻的测量值小于真实值 |
15.如图所示为某质点的速度-时间图象,则下列说法中正确的是( )


| A. | 在0~6s内,质点做匀变速直线运动 | B. | 在t=12s末,质点的加速度为-1m/s2 | ||
| C. | 在6~10s内,质点处于静止状态 | D. | 在4s末,质点运动方向改变 |
12.一个质点做方向不变的直线运动加速度的方向始终与速度方向相同,但加速度大小逐渐减小直至为零,在此过程中( )
| A. | 位移逐渐减小,当加速度减小到零吋,位移将不再减小 | |
| B. | 速度逐渐减小,当加速度减小到零时,速度达到最小值 | |
| C. | 速度逐渐增大,当加速度减小到零时,速度达到最大值 | |
| D. | 位移逐渐增大,当加速度减小到零时,位移将不再增大 |

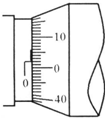 在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=0.810m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率.
在“测定金属的电阻率”的实验中,用螺旋测微器测量金属丝直径时的刻度位置如图所示,用米尺测量金属丝的长度l=0.810m.金属丝的电阻大约为4Ω.先用伏安法测出金属丝的电阻,然后根据电阻定律计算出该金属材料的电阻率.