题目内容
16.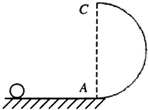 如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道进入竖直圆轨道,通过最高点C时对轨道的压力为其重力的3倍.不计空气阻力,g取10m/s2.求:
如图所示,半径R=0.9m的光滑的半圆轨道固定在竖直平面内,直径AC竖直,下端A与光滑的水平轨道相切.一个质量m=1kg的小球沿水平轨道进入竖直圆轨道,通过最高点C时对轨道的压力为其重力的3倍.不计空气阻力,g取10m/s2.求:(1)小球在A点的速度大小vA;
(2)小球的落地点到A点的距离s;
(3)小球的落地前瞬间重力的瞬时功率PG.
分析 (1)由向心力公式可求得最高点的速度,对AC过程由机械能守恒定律可求得A点的速度;
(2)小球离开C点后做平抛运动,由平抛运动的规律可求得水平距离s;
(3)求出落地时的竖直分速度,再由功率公式即可求得重力的功率.
解答 解:(1)设小球通过最高点C时的速度为vc,根据牛顿第二定律,有
$mg+3mg=m\frac{v_c^2}{R}$
解得:vc=6m/s
设小球在A点的速度大小为vA,以地面为参考平面,根据机械能守恒定律,有:
$\frac{1}{2}mv_A^2=\frac{1}{2}mv_C^2+mg•2R$
解得:${v_A}=\sqrt{v_c^2+4gR}=6\sqrt{2}m/s=8.5m/s$
(2)小球离开C点后作平抛运动,根据 $2R=\frac{1}{2}g{t^2}$
它在空中运动的时间为 t=0.6s
小球的落地点到A点的距离为 s=vc•t=3.6m
(3)小球落地前竖直速度vy=gt=6m/s
小球的落地前瞬间重力的瞬时功率PG=mgvy=6W
答:
(1)小球在A点的速度大小vA是8.5m/s.
(2)小球的落地点到A点的距离s是3.6m;
(3)小球的落地前瞬间重力的瞬时功率PG是6W.
点评 本题主要考查了向心力公式、机械能守恒定律及平抛运动基本公式的直接应用,对于圆周运动的动力学,关键分析什么力提供向心力,对于圆周光滑情形,要考虑运用机械能守恒定律解题.

练习册系列答案
相关题目
6.升降机中弹簧测力计下挂一重物,重物的质量为5kg,而弹簧测力计的示数为25N,那么升降机的运动可能是( )
| A. | 竖直向上匀加速运动 | B. | 竖直向下匀加速运动 | ||
| C. | 竖直向上匀减速运动 | D. | 竖直向下匀减速运动 |
7.关于重力势能的几种理解,正确的是( )
| A. | 重力对物体做正功时.物体的重力势能减小 | |
| B. | 放在地面上的物体,它的重力势能一定等于零 | |
| C. | 在不同高度将某一物体抛出.落地时重力势能相等 | |
| D. | 相对不同的参考平面,物体具有不同数值的重力势能,但并不影响有关重力势能问题 |
4.我国“蛟龙号”深潜器经过多次试验,终于在2012年6月24日以7020m深度创下世界最新纪录(国外最深不超过6500m).这预示着它可以征服全球99.8%的海底世界.假设在某次实验时,深潜器内的显示屏上显示出了从水面开始下潜到最后返回水面10min内全过程的深度曲线(a)和速度图象(b),则下列说法中正确的是( )


| A. | (a)图中h3代表本次最大深度,应为360m | |
| B. | 全过程中最大加速度是0.025m/s2 | |
| C. | 潜水员感到超重发生在3-4min和6-8min的时间段内 | |
| D. | 潜水器在4-6min时间段内处于匀速运动状态 |
11.关于温度的下列说法,正确的是( )
| A. | 温度是物体的冷热程度的标志 | |
| B. | 温度是物体内能的标志 | |
| C. | 温度是物体分子势能的标志 | |
| D. | 气体的温度是气体分子平均动能的标志 |
1.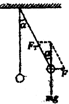 如图所示,一轻绳上端固定,下端系一个质量为m的小球.现对小球施加一个F=mg的水平拉力,使小球偏离竖直位置并保持静止,则轻绳与竖直方向的夹角为( )
如图所示,一轻绳上端固定,下端系一个质量为m的小球.现对小球施加一个F=mg的水平拉力,使小球偏离竖直位置并保持静止,则轻绳与竖直方向的夹角为( )
 如图所示,一轻绳上端固定,下端系一个质量为m的小球.现对小球施加一个F=mg的水平拉力,使小球偏离竖直位置并保持静止,则轻绳与竖直方向的夹角为( )
如图所示,一轻绳上端固定,下端系一个质量为m的小球.现对小球施加一个F=mg的水平拉力,使小球偏离竖直位置并保持静止,则轻绳与竖直方向的夹角为( )| A. | 30° | B. | 37° | C. | 45° | D. | 60° |
8.关于匀速圆周运动的说法正确的是( )
| A. | 匀速圆周运动一定是匀速运动 | B. | 匀速圆周运动的合力可能为恒力 | ||
| C. | 匀速圆周运动是加速度不变的运动 | D. | 匀速圆周运动是变加速运动 |
5.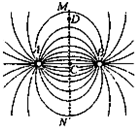 A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
 A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )
A、B两个点电荷在真空中所产生电场的电场线(方向未标出)如图所示.图中C点为两点电荷连线的中点,MN为两点电荷连线的中垂线,D为中垂线上的一点,电场线的分布关于MN左右对称.则下列说法中正确的是( )| A. | 这两点电荷一定是等量异种电荷 | |
| B. | 这两点电荷一定等量同种电荷 | |
| C. | 一电子从C点移到到D点电场力不做功 | |
| D. | C点的电场强度比D点的电场强度大 |
6. 如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
 如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )
如图所示,竖直面有两个$\frac{3}{4}$圆形导轨固定在一水平地面上,半径R相同,A轨道由金属凹槽制成,B轨道由金属圆管制成,均可视为光滑轨道.在两轨道右侧的正上方将质量均为m的金属小球A和B由静止释放,小球距离地面的高度分别用hA和hB表示,则下列说法正确的是( )| A. | 适当调整hA和hB,均可使两小球从轨道最高点飞出后,恰好落在轨道右端口处 | |
| B. | 若hA=hB=2R,则两小球在轨道最低点对轨道的压力为4mg | |
| C. | 若hA=hB=R,则两小球都能上升到离地高度为R的位置 | |
| D. | 若使小球沿轨道运动并且能从最高点飞出,A小球的最小高度为$\frac{5B}{2}$,B小球在hB>2R的任何高度均可 |