题目内容
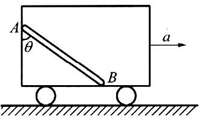 如图所示,在以一定加速度a行驶的车厢内,有一长为L、质量为m的棒AB靠在光滑的后壁上,棒与厢底面之间的动摩擦因数为μ,为了使棒不滑动,棒与竖直平面所成的夹角为θ,则tanθ的值可取( )
如图所示,在以一定加速度a行驶的车厢内,有一长为L、质量为m的棒AB靠在光滑的后壁上,棒与厢底面之间的动摩擦因数为μ,为了使棒不滑动,棒与竖直平面所成的夹角为θ,则tanθ的值可取( )分析:棒与车具有相同的加速度,当棒与竖直平面所成的夹角最大时,有向左的最大静摩擦力,夹角最小时,有向右的最大静摩擦力,根据牛顿第二定律求出车厢后壁对棒的弹力,在根据力矩平衡求出临界的角度.
解答:解:设在A、B处的弹力大小各是FA、FB,在B处静摩擦力大小是 f.
当夹角θ取较大的数值θ大时,棒将发生A向下、B向右滑动,这时 f 的方向是水平向左.
由牛顿第二定律得:FA1-f=ma 且 f=μFB,FB=mg (竖直方向不动)
得 FA1=m(a+μg)
车厢是非惯性系,在车厢里看棒受到非惯性力F惯=ma
以B点为轴,用合力矩为0得 FA1Lcosθ大=mg
sinθ大+ma
cosθ
所以 tanθ大=
=
θ大=arc tan
.
当夹角θ取较小的数值θ小时,棒将发生A向上、B向左滑动,这时 f 的方向是水平向右.
由牛顿第二定律得 FA2+f=ma 且 f=μFB,FB=mg (竖直方向不动)
得 FA2=m(a-μg)
以B点为轴,用合力矩为0得 FA2Lcosθ小=mg
sinθ小+ma
cosθ
所以 tanθ小=
=
θ小=arc tan
综上所述,夹角θ应在的范围是:
arc tan
≤θ≤arc tan
.故A、C、D正确,B错误.
故选ACD.
当夹角θ取较大的数值θ大时,棒将发生A向下、B向右滑动,这时 f 的方向是水平向左.
由牛顿第二定律得:FA1-f=ma 且 f=μFB,FB=mg (竖直方向不动)
得 FA1=m(a+μg)
车厢是非惯性系,在车厢里看棒受到非惯性力F惯=ma
以B点为轴,用合力矩为0得 FA1Lcosθ大=mg
| L |
| 2 |
| L |
| 2 |
所以 tanθ大=
| 2FA1 |
| mg |
| a+2μg |
| g |
θ大=arc tan
| a+2μg |
| g |
当夹角θ取较小的数值θ小时,棒将发生A向上、B向左滑动,这时 f 的方向是水平向右.
由牛顿第二定律得 FA2+f=ma 且 f=μFB,FB=mg (竖直方向不动)
得 FA2=m(a-μg)
以B点为轴,用合力矩为0得 FA2Lcosθ小=mg
| L |
| 2 |
| L |
| 2 |
所以 tanθ小=
| 2FA2 |
| mg |
| a-2μg |
| g |
θ小=arc tan
| a-2μg |
| g |
综上所述,夹角θ应在的范围是:
arc tan
| a-2μg |
| g |
| a+2μg |
| g |
故选ACD.
点评:本题综合考查了牛顿第二定律和力矩平衡,综合性较强,以及考查了非惯性系问题,增加了题目的难度,要考虑棒会受到非惯性力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
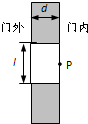
如图所示,在真空室中有两块长为L的水平金属板,板间的距离为d,有一质量为m的小油滴,电荷量为q,自上极板的表面处从左侧以一初速度v0进入板间,当它运动到两极板间区域的正中央时,给两极板加电压U,使小油滴受到向上的电场力开始做匀速直线运动,则 ( )
A.小油滴进入板间的初速度 |
B.两极板所加电压为 |
| C.小油滴一定从下极板的右侧射出 |
D.小油滴一定会打在下极板距离右侧 处 处 |

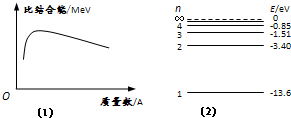 A.小质量数的原子核质量亏损最大
A.小质量数的原子核质量亏损最大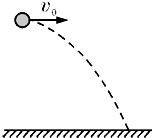 如图所示,在距地面一定高度的位置以初速度v0向右水平抛出一个质量为m、电荷量为q的带负电小球,小球的落地点与抛出点之间有一段相应的水平距离(水平射程).若在空间上加一竖直方向的匀强电场,使小球的水平射程变为原来的一半,求此电场的场强大小和方向.
如图所示,在距地面一定高度的位置以初速度v0向右水平抛出一个质量为m、电荷量为q的带负电小球,小球的落地点与抛出点之间有一段相应的水平距离(水平射程).若在空间上加一竖直方向的匀强电场,使小球的水平射程变为原来的一半,求此电场的场强大小和方向.





 处
处