题目内容
某实验小组采用图示的装置探究“牛顿第二定律”即探究加速度a与合力F、质量M的关系.实验中,小车碰到制动装置时,钩码尚未到达地面.
(1)为了把细绳对小车的拉力视为小车的合外力,要完成的一个重要步骤是
(2)为使图示中钩码的总重力大小视为细绳的拉力大小,须满足的条件是钩码的总质量
(3)一组同学在做小车加速度与小车质量的关系实验时,保持钩码的质量一定,改变小车的总质量,测出相应的加速度.采用图象法处理数据.为了比较容易地检查出加速度a与小车的总质量M之间的关系,应作出a与
的图象.
(4)甲同学根据测量数据作出的a-F图象如图所示,说明实验中存在的问题是
(1)为了把细绳对小车的拉力视为小车的合外力,要完成的一个重要步骤是
平衡摩擦力
平衡摩擦力
;(2)为使图示中钩码的总重力大小视为细绳的拉力大小,须满足的条件是钩码的总质量
远小于
远小于
小车的总质量(填“大于”、“小于”、“远大于”或“远小于”).(3)一组同学在做小车加速度与小车质量的关系实验时,保持钩码的质量一定,改变小车的总质量,测出相应的加速度.采用图象法处理数据.为了比较容易地检查出加速度a与小车的总质量M之间的关系,应作出a与
| 1 |
| M |
| 1 |
| M |
(4)甲同学根据测量数据作出的a-F图象如图所示,说明实验中存在的问题是
平衡摩擦力时斜面的倾角过大
平衡摩擦力时斜面的倾角过大
. 
分析:(1)小车下滑时受到重力、细线的拉力、支持力和摩擦力,要使拉力等于合力,则应该用重力的下滑分量来平衡摩擦力,故可以将长木板的一段垫高;
(2)重物加速下滑,处于失重状态,其对细线的拉力小于重力,要使其对细线的拉力近似等于重力,应该使加速度减小,即重物的质量应该远小于小车的质量.
(3)反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系;正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系.
(4)图2中图象与纵轴的截距大于0,说明在拉力等于0时,就已经有加速度.
(2)重物加速下滑,处于失重状态,其对细线的拉力小于重力,要使其对细线的拉力近似等于重力,应该使加速度减小,即重物的质量应该远小于小车的质量.
(3)反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系;正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系.
(4)图2中图象与纵轴的截距大于0,说明在拉力等于0时,就已经有加速度.
解答:解:(1)小车下滑时受到重力、细线的拉力、支持力和摩擦力,要使拉力等于合力,则应该用重力的下滑分量来平衡摩擦力;
(2)重物加速下滑,处于失重状态,其对细线的拉力小于重力,设拉力为T,根据牛顿第二定律,有
对重物,有 mg-T=ma
对小车,有 T=Ma
解得
T=
mg
故当M>>m时,有T≈mg
(3)根据牛顿第二定律F=Ma,a与M成反比,而反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系,故不能作a-M图象;
但a=
,故a与
成正比,而正比例函数图象是过坐标原点的一条直线,就比较容易判定自变量和因变量之间的关系,故应作a-
图象.
(4)图2中图象与纵轴的截距大于0,说明在拉力等于0时,就已经有加速度,说明平衡摩擦力时斜面的倾角过大.
故答案为:(1)平衡摩擦力;(2)远小于;(3)
;(4)平衡摩擦力时斜面的倾角过大
(2)重物加速下滑,处于失重状态,其对细线的拉力小于重力,设拉力为T,根据牛顿第二定律,有
对重物,有 mg-T=ma
对小车,有 T=Ma
解得
T=
| M |
| M+m |
故当M>>m时,有T≈mg
(3)根据牛顿第二定律F=Ma,a与M成反比,而反比例函数图象是曲线,而根据曲线很难判定出自变量和因变量之间的关系,故不能作a-M图象;
但a=
| F |
| M |
| 1 |
| M |
| 1 |
| M |
(4)图2中图象与纵轴的截距大于0,说明在拉力等于0时,就已经有加速度,说明平衡摩擦力时斜面的倾角过大.
故答案为:(1)平衡摩擦力;(2)远小于;(3)
| 1 |
| M |
点评:只要真正掌握了实验原理就能顺利解决此类实验题目,而实验步骤,实验数据的处理都与实验原理有关,故要加强对实验原理的学习和掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某实验小组采用图示的装置探究“恒力拉动下小车的运动情况”,图中小车中可放置砝码,实验中,小车碰到制动装置时,钩码尚未到达地面,打点针时器工作频率为50 Hz.
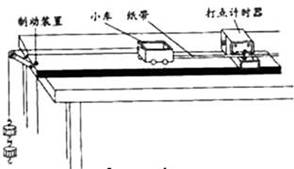
(1)实验的部分步骤如下,请将步骤②补充完整:
①在小车中放入砝码,把纸带穿过打点计时器,连在小车后端,用细线连接小车和钩码;
②将小车停在打点计时器附近, , ,小车拖动纸带,打点计时器在纸带上打下一系列点,断开开关,取下纸带。
③改变钩码或小车中砝码的数量,更换纸带,重复②的操作。
(2)下图是钩码质量为0.03 kg,砝码质量为0.02 kg时得到的一条纸带,在纸带上选择起始点0及A、B、C、D和E五个计数点,通过数据处理可获得各计数点对应时刻小车的瞬时速度v,

下表是纸带的一些测量结果,根据上面的插图可知OA的长度 cm,OC的长度 cm;
根据下表的数据可知,打下计数点C时,小车的瞬时速度是 m/s。
|
测量点 |
S/cm |
v/(m·s-1) |
|
0 |
-- |
0.35 |
|
A |
|
0.40 |
|
B |
-- |
0.45 |
|
C |
|
|
|
D |
-- |
0.54 |
|
E |
-- |
0.60 |
(3)由纸带和测量数据不难看出,纸带的 (“左”或“右”)端是系小车的。
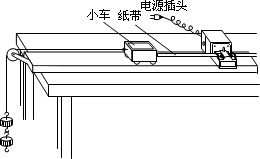
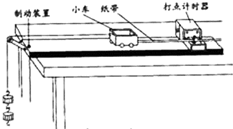 某实验小组采用图示的装置“探究恒力做功与物体的动能改变量的关系”,图中小车中可放置砝码,实验中,小车碰到制动装置时,尚未到达地面,打点针时器工作频率为 50Hz.实验中备有下列器材:A.打点计时器 B.天平 C.秒表 D.电池 E.纸带 F.细线、钩码、小车 G.长轨道
某实验小组采用图示的装置“探究恒力做功与物体的动能改变量的关系”,图中小车中可放置砝码,实验中,小车碰到制动装置时,尚未到达地面,打点针时器工作频率为 50Hz.实验中备有下列器材:A.打点计时器 B.天平 C.秒表 D.电池 E.纸带 F.细线、钩码、小车 G.长轨道