题目内容
(8分)两根长度均为L="5" m的杆子竖直放置,如图所示, A下端离地高度为H="20" m ,B下端开始放在水平地面上,将A从静止开始释放,同时给B一个竖直向上的初速度V0 ="20" m/s,空中运动过程两杆一直均保持竖直且不相碰 (g取10m/s2) ,求:
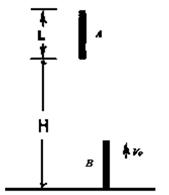
(1)两杆从出发到开始相遇需多长时间?
(2)两杆从开始相遇到相遇结束需多长时间?

(1)两杆从出发到开始相遇需多长时间?
(2)两杆从开始相遇到相遇结束需多长时间?
(1)0.75s;(2)0.5s。
试题分析:(1)设两杆从出发到开始相遇的时间为t,
则A杆下落的高度为xA=
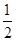 gt2,B杆上升的高度为xB=v0t-
gt2,B杆上升的高度为xB=v0t-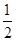 gt2,
gt2,故存在xA+xB=15m,即v0t=15m,解得t=
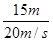 =0.75s。
=0.75s。(2)设两杆从开始相遇到相遇结束需要的时间为T,
则A杆相遇时的速度为vA=gt=7.5m/s,
相遇到结束时A杆下降的距离sA=vAT+
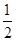 gT2
gT2B杆相遇时的速度为vB=20m/s-7.5m/s=12.5m/s
相遇到结束时B杆上升的高度sB=vBT-
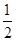 gT2,
gT2,故sA+sB=2L
则vAT+vBT=10m,解之得T=0.5s。

练习册系列答案
相关题目


 ,下列说法正确的是
,下列说法正确的是