题目内容
【题目】如图所示,质量为m=1.1kg的物体(可视为质点)用细绳拴住,放在水平传送带的右端,物体和传送带之间的动摩擦因数μ=0.5,传送带的长度L=5m,当传送带以v=5m/s的速度做逆时针转动时,绳与水平方向的夹角θ=37°.已知:g=l0m/s2,sin37°=0.6,cos37°=0.8.求:
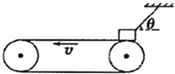
(1)传送带稳定运动时绳子的拉力T;
(2)某时刻剪断绳子,求物体运动至传送带最左端所用时间;
【答案】(1)5N(2)1.5s
【解析】
试题分析:(1)传送带稳定运动时,物体处于平衡状态,有:T cosθ=μ(mg-Tsinθ)
带入数据解得:T=5N
(2)剪断绳子后,根据牛顿第二定律有:μmg=ma
代入数据求得:a=5m/s2
匀加速的时间为:![]()
位移为:s1=![]() at2=
at2=![]() ×5×12=2.5 m
×5×12=2.5 m
则匀速运动的时间为:![]()
总时间为:t=t1+t2=1+0.5=1.5s

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目