题目内容
16. 如图所示,竖直放置的两根足够长的光滑金属导轨相距为L,导轨的两端分别与电源(串有一滑动变阻器R)、定值电阻、电容器(原来不带电)和开关K相连.整个空间充满了垂直于导轨平面向外的匀强磁场,其磁感应强度的大小为B.一质量为m,电阻不计的金属棒ab横跨在导轨上.已知电源电动势为E,内阻为r,电容器的电容为C,定值电阻的阻值为R0,不计导轨的电阻.
如图所示,竖直放置的两根足够长的光滑金属导轨相距为L,导轨的两端分别与电源(串有一滑动变阻器R)、定值电阻、电容器(原来不带电)和开关K相连.整个空间充满了垂直于导轨平面向外的匀强磁场,其磁感应强度的大小为B.一质量为m,电阻不计的金属棒ab横跨在导轨上.已知电源电动势为E,内阻为r,电容器的电容为C,定值电阻的阻值为R0,不计导轨的电阻.(1)当K接1时,金属棒ab在磁场中恰好保持静止,则滑动变阻器接入电路的阻值R多大?
(2)当K接2后,金属棒ab从静止开始下落,下落距离s时达到稳定速度,则此稳定速度的大小为多大?下落s的过程中所需的时间为多少?
(3)若在将ab棒由静止释放的同时,将电键K接到3.试通过推导说明ab棒此后的运动性质如何?求ab再下落距离s时,电容器储存的电能是多少?(设电容器不漏电,此时电容器还没有被击穿)
分析 (1)当K接1时,金属棒ab在磁场中恰好保持静止,棒的重力与安培力平衡,由平衡条件和安培力公式列式,可求出电路中的电流,再根据欧姆定律求R;
(2)当K接2后,金属棒ab从静止开始下落,先做加速度减小的变加速运动,后做匀速运动,达到稳定状态,根据重力的功率等于电功率列式求速度.根据动量定理和法拉第定律列式求时间.
(3)ab达到稳定速度后,将开关K突然接到3,电容器充电,电路中充电电流,ab棒受到安培力,安培力的瞬时表达式F=BiL,i=$\frac{△Q}{△t}$=$\frac{C△U}{△t}$,又U=E=BLv,再结合牛顿第二定律求得瞬时加速度,即可判断棒的运动性质.根据能量守恒求电容器储存的电能.
解答 解:(1)k接到1位置时,有 $I=\frac{E}{R+r}$
由平衡条件得 mg=BIL,
得 $I=\frac{mg}{BL}$
联立得 $R=\frac{E}{I}-r=\frac{EBL}{mg}-r$
(2)k接到2位置时,稳定时,有$mg=B\frac{BLv}{R_0}L$,$v=\frac{{mg{R_0}}}{{{B^2}{L^2}}}$
根据牛顿第二定律得 $mg-B\frac{BLv}{R_0}L=ma$,得$a=g-\frac{{{B^2}{L^2}}}{{m{R_0}}}v$
由$△v=a△t=g△t-\frac{{{B^2}{L^2}}}{{m{R_0}}}v△t$得
$\sum△v=\sum a△t=g\sum△t-\frac{{{B^2}{L^2}}}{{m{R_0}}}\sum v△t$
可得 $v=gt-\frac{{{B^2}{L^2}}}{{m{R_0}}}s$
所以时间 $t=\frac{v}{g}+\frac{{{B^2}{L^2}s}}{{mg{R_0}}}=\frac{{m{R_0}}}{{{B^2}{L^2}}}+\frac{{{B^2}{L^2}s}}{{mg{R_0}}}$
(3)k接到3位置时,ab棒做匀加速运动mg-BIL=ma
电流为 $I=\frac{△Q}{t}=\frac{C△U}{t}=\frac{CBL△v}{t}$
由牛顿第二定律得 $mg-B\frac{CBL△v}{△t}L=ma$
得 $a=\frac{m}{{m+C{B^2}{L^2}}}g$
可见棒的加速度不变,做匀加速直线运动.
设下落距离s时的速度为v
则
$\begin{array}{l}{v^2}=2as\\ v=\sqrt{2as}\end{array}$
此时电容器储存的电能为E,则得
$\begin{array}{l}E=mgs-\frac{1}{2}m{v^2}\\=\frac{{mgsC{B^2}{L^2}}}{{m+C{B^2}{L^2}}}\end{array}$
答:
(1)滑动变阻器接入电路的阻值R为$\frac{EBL}{mg}$-r.
(2)稳定速度的大小为$\frac{mg{R}_{0}}{{B}^{2}{L}^{2}}$,下落s的过程中所需的时间为$\frac{m{R}_{0}}{{B}^{2}{L}^{2}}$+$\frac{{B}^{2}{L}^{2}s}{mg{R}_{0}}$.
(3)棒做加速度为$\frac{m}{m+C{B}^{2}{L}^{2}}$g的匀加速直线运动,ab再下落距离s时,电容器储存的电能为$\frac{mgsC{B}^{2}{L}^{2}}{m+C{B}^{2}{L}^{2}}$.
点评 本题是电磁感应与电路、力学知识的综合,关键要会推导加速度的表达式,通过分析棒的受力情况,确定其运动情况.

 比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )| A. | 这种车可能是国产高档车 | B. | 这种车可能是国产中档车 | ||
| C. | 这种车可能是国产低档车 | D. | 条件不足,不能判断 |
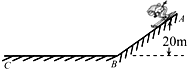 如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )
如图所示,某同学乘雪撬从雪坡经A点滑至B点,接着沿水平路面滑至C点停止.人与雪撬的总质量为60kg.表中记录了沿坡滑下过程中的有关数据,根据图表中提供的数据下列判断正确的是(设人与雪撬在BC段所受阻力恒定,g取10m/s2)( )| 位置 | A | B | C |
| 速度(m/s) | 2.0 | 12.0 | 0 |
| 时刻(s) | 0 | 4 | 10 |
| A. | 人与雪橇从A到B的过程中,重力做功为4.2×l03J | |
| B. | 人与雪撬从A到B的过程中,损失的机械能为1.2×104J | |
| C. | 0到4s这段时间内,合外力对人与雪橇做的功为4.2×103J | |
| D. | 0到10s这段时间内,人与雪撬重力做功的平均功率为1.2×103W |
| A. | 电子的发现说明原子中一定还有带正电的部分 | |
| B. | J.J.汤姆孙发现了电子,并提出了电子绕核运动 | |
| C. | 在验证电子波动性的实验中,电子的动能越大,电子的衍射现象越明显 | |
| D. | 验证电子波动性的实验中,若用相同动能的质子代替电子,衍射现象将更加明显 |
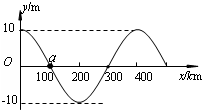 北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )
北京时间2011年3月11日13时46分日本仙台以东地区发生里氏9.0级强烈地震,震源深度24km,地震随后引发10m高海啸,形成强大的波浪,向前推进,将沿海地带一一淹没,并于美国当地时间3月11日凌晨3时左右,抵达5700多公里以外的夏威夷群岛,造成至少3亿美元财产损失.海啸在海洋的传播速度大约每小时500到600km,是地震波传播速度的$\frac{1}{25}$左右.下列说法中正确的是( )| A. | 海啸波是电磁波 | |
| B. | 美国夏威夷发生的海啸是日本发生的地震,并将该处的海水传到了美国夏威夷而引起的 | |
| C. | 可以利用地震波传播速度与海啸传播速度的差别造成的时间差进行海啸预警 | |
| D. | 设如图所示海啸波沿+x轴方向传播,图中a点经$\frac{1}{4}$周期时将到达10 m高的波峰处 |
| A. | 物体沿斜面匀速下滑 | B. | 物体沿斜面匀减速上滑 | ||
| C. | 物体沿斜面匀速上滑 | D. | 物体沿斜面匀减速下滑 |
 某学校研究性学习小组想测量木块与木板之间的动摩擦因数.其中一位同学把木板固定在斜面上,他让木块从斜面上端由静止开始匀加速下滑,如图所示,他使用的实验器材仅限于:
某学校研究性学习小组想测量木块与木板之间的动摩擦因数.其中一位同学把木板固定在斜面上,他让木块从斜面上端由静止开始匀加速下滑,如图所示,他使用的实验器材仅限于: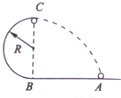 如图所示,AB为一长L=1.2m的光滑水平轨道,BC为竖直平面内半径R=0.4m的光滑半圆轨通,两轨道在B点相切.一小球从A向B做匀速直线运动,冲上半圆轨道,到达最高点C后水平抛出,最后落回到原来的出发点A,求:小球在A点运动的速度为多大.
如图所示,AB为一长L=1.2m的光滑水平轨道,BC为竖直平面内半径R=0.4m的光滑半圆轨通,两轨道在B点相切.一小球从A向B做匀速直线运动,冲上半圆轨道,到达最高点C后水平抛出,最后落回到原来的出发点A,求:小球在A点运动的速度为多大.