题目内容
如图所示，固定于水平桌面上足够长的两平行导轨PO、MN，PQ、MN的电阻不计，间距为d=0.5m.P、M两端接有一只理想电压表，整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中.电阻均为r=0.1Ω，质量分别为m1=300g和m2=500g的两金属棒L1、L2平行的搁在光滑导轨上，现固定棒L1，L2在水平恒力F=0.8N的作用下，由静止开始做加速运动，试求:
(1)当电压表的读数为U=0.2V时，棒L2的加速度多大？
(2)棒L2能达到的最大速度vm.
(3)若在棒L2达到最大速度vm时撤去外力F，并同时释放棒L1，求棒L2达到稳定时的速度值.
(4)若固定棒L1，当棒L2的速度为v，且离开棒L1距离为S的同时，撤去恒力F，为保持棒L2做匀速运动，可以采用将B从原值(B0=0.2T)逐渐减小的方法，则磁感应强度B应怎样随时间变化(写出B与时间t的关系式)？
(1)1.2m/s2 (2)16m/s (3)10m/s (4) 
解析:
解:(1)∵L1与L2串联
∴流过L2的电流为:
① (2分)
L2所受安培力为:F′=BdI=0.2N ② (2分)
∴
③ (2分)
(2)当L2所受安培力F安=F时，棒有最大速度vm，此时电路中电流为Im.
则：F安=BdIm ④ (1分)
⑤ (1分)
F安=F ⑥ (1分)
由④⑤⑥得：
⑦ (2分)
(3)撤去F后，棒L2做减速运动，L1做加速运动，当两棒达到共同速度v共时，L2有稳定速度，对此过程有：
⑧ (2分)
∴
⑨ (2分)
(4)要使L2保持匀速运动，回路中磁通量必须保持不变，设撤去恒力F时磁感应强度为B0，t时刻磁感应强度为Bt，则：
B0dS=Btd（S+vt） ⑩ (3分)
∴ (2分)
如图所示，固定于水平桌面上的金属框架cdef，处在竖直向下的匀强磁场中，金属棒ab搁在框架上，可无摩擦滑动．此时abed构成一个边长为L的正方形，棒的电阻为r，其余部分电阻不计．开始时磁感应强度为B0．
（2010?盐城三模）如图所示，固定于水平面的U型金属导轨abcd，电阻不计，导轨间距L=1.0m，左端接有电阻R=2Ω．金属杆PQ的质量m=0.2Kg，电阻r=1Ω，与导轨间动摩擦因数μ=0.2，滑动时保持与导轨垂直．在水平面上建立x0y坐标系，x≥0的空间存在竖直向下的磁场，磁感应强度仅随横坐标x变化．金属杆受水平恒力F=2.4N的作用，从坐标原点开始以初速度v0=1.0m/s向右作匀加速运动，经t1=0.4s到达x1=0.8m处，g取10m/s2．
如图所示，固定于水平桌面上足够长的两平行导轨PO、MN，PQ、MN的电阻不计，间距为d=0.5m．P、M两端接有一只理想电压表，整个装置处于竖直向下的磁感应强度B=0.2T的匀强磁场中．电阻均为r=0.1Ω，质量分别为m1=300g和m2=500g的两金属棒L1、L2平行的搁在光滑导轨上，现固定棒L1，L2在水平恒力F=0.8N的作用下，由静止开始做加速运动，试求：
（2010?宿州二模）如图所示，固定于水平面上的金属架CDEF处在竖直向下的匀强磁场中，金属棒MN沿框架以某一速度向右做匀速运动．t=0时，磁感应强度为B0，此时MN到达的位置恰好使MDEN构成一个边长为L的正方形．为使MN棒中不产生感应电流，从t=0开始，磁感应强度B随时间t的变化的图象正确的是（ ）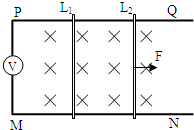
如图所示，固定于水平桌面上足够长的两平行导轨PQ、MN，PQ、MN的电阻不计，间距为d=0.5m，PM两端接有一理想电压表，整个装置处于竖直向下的匀强磁场中，磁感应强度为B=0.2T，电阻均为R=0.1Ω、质量分别为m1=300g 和m2=500g的两金属棒L1、L2平行地搁在光滑的导轨上，现固定L1，L2在水平恒力F=0.8N的作用下，由静止开始作加速运动．试求：