题目内容
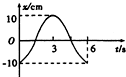 如图所示是单摆做简谐运动的图象,以向右为正方向,则由图可知:
如图所示是单摆做简谐运动的图象,以向右为正方向,则由图可知:(1)单摆是从
最左端
最左端
开始起振,(2)摆长l=
9m
9m
(3)摆球从起振经过9s,经过的路程是
60cm
60cm
(4)摆球在t=63s末的位移是
10cm
10cm
.分析:(1)由t=0时刻单摆的位移,分析开始振动的位置;
(2)由图读出摆长,由单摆周期公式T=2π
求出摆长;
(3)摆球在一个周期通过的路程是四个振幅,根据时间与周期的关系,求解路程;
(4)分析摆球在t=63s末的位置,即可确定位移.
(2)由图读出摆长,由单摆周期公式T=2π
|
(3)摆球在一个周期通过的路程是四个振幅,根据时间与周期的关系,求解路程;
(4)分析摆球在t=63s末的位置,即可确定位移.
解答:解:
(1)由图知,t=0时刻,x=-10cm,而题中的正方向是向右,说明开始时单摆是从最左端开始起振;
(2)由图知,单摆振动的周期为T=6s,由单摆周期公式T=2π
得
l=
=
m≈9m
(3)时间t=9s=1.5T,而摆球在一个周期通过的路程是四个振幅,所以摆球从起振经过9s,经过的路程是S=6A=60cm.
(4)n=
=
=10
,则t=63s时,摆球在t=63s末的位移与t=0时刻相反,即为10cm.
故答案为:
(1)最左端;(负最大位移处)
(2)9m;
(3)60cm;
(4)10cm.
(1)由图知,t=0时刻,x=-10cm,而题中的正方向是向右,说明开始时单摆是从最左端开始起振;
(2)由图知,单摆振动的周期为T=6s,由单摆周期公式T=2π
|
l=
| gT2 |
| 4π2 |
| 9.8×62 |
| 4×3.142 |
(3)时间t=9s=1.5T,而摆球在一个周期通过的路程是四个振幅,所以摆球从起振经过9s,经过的路程是S=6A=60cm.
(4)n=
| t |
| T |
| 63 |
| 6 |
| 1 |
| 2 |
故答案为:
(1)最左端;(负最大位移处)
(2)9m;
(3)60cm;
(4)10cm.
点评:本题考查基本的读图能力,掌握单摆的周期公式和单摆的周期性,分析和计算摆球的路程和位移.

练习册系列答案
相关题目
 (2009?汕头一模)(1)以下说法正确的是
(2009?汕头一模)(1)以下说法正确的是 如图所示的单摆,摆长为l=40cm,摆球在t=0时刻从右侧最高点释放做简谐振动,则当t=1s时,小球的运动情况是( )
如图所示的单摆,摆长为l=40cm,摆球在t=0时刻从右侧最高点释放做简谐振动,则当t=1s时,小球的运动情况是( )

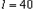 cm,摆球在
cm,摆球在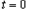 时刻从右侧最高点释放做简谐振动,则当
时刻从右侧最高点释放做简谐振动,则当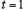 s时,小球的运动情况是
s时,小球的运动情况是