题目内容
15. 如图所示,质量分别为m1和m2的两个小球A、B在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞,碰后B球被右侧的墙原速弹回,又与A球相碰,碰后两球都静止.
如图所示,质量分别为m1和m2的两个小球A、B在光滑的水平面上分别以速度v1、v2同向运动并发生对心碰撞,碰后B球被右侧的墙原速弹回,又与A球相碰,碰后两球都静止.①求两球第一次碰撞后B球的速度.
②B与竖直墙面碰撞过程中,墙对B球的冲量大小及方向?
分析 ①两球碰撞过程系统动量守恒,应用动量守恒定律可以求出碰撞后球的速度.
②对B球,应用动量定律可以求出墙对B的冲量.
解答 解:①设第一次碰撞后A球的速度为vA,B球的速度为vB,碰撞过程系统动量守恒,以向右为正方向,由动量守恒定律得:
m1v1+m2v2=m1vA+m2vB,
第二次碰撞后A、B球的速度为零,A、B组成的系统动量守恒,以向右为正方向,由动量守恒定律的:
m1vA-m2vB=0,
解得:vB=$\frac{{m}_{1}{v}_{1}+{m}_{2}{v}_{2}}{2{m}_{2}}$;
②设水平向右为正方向,对B球,由动量定理可得:
I=-m2vB-m2vB=-(m1v1+m2v2),
即墙对B球的冲量大小为:I=m1v1+m2v2,方向:水平向左.
答:①两球第一次碰撞后B球的速度为$\frac{{m}_{1}{v}_{1}+{m}_{2}{v}_{2}}{2{m}_{2}}$.
②B与竖直墙面碰撞过程中,墙对B球的冲量大小为:m1v1+m2v2,方向水平向左.
点评 本题考查了求球的速度、墙对球的冲量,分析清楚球的运动过程,应用动量守恒定律、动量定理即可正确解题,解题时要注意各物理量的方向.

练习册系列答案
相关题目
6. 在双缝干涉实验中,双缝到光屏上P点的距离之差0.6μm,若分别用频率为f1=5.0×1014Hz和f2=7.5×1014Hz的单色光垂直照射双缝,则 P点出现明、暗条纹的情况是( )
在双缝干涉实验中,双缝到光屏上P点的距离之差0.6μm,若分别用频率为f1=5.0×1014Hz和f2=7.5×1014Hz的单色光垂直照射双缝,则 P点出现明、暗条纹的情况是( )
 在双缝干涉实验中,双缝到光屏上P点的距离之差0.6μm,若分别用频率为f1=5.0×1014Hz和f2=7.5×1014Hz的单色光垂直照射双缝,则 P点出现明、暗条纹的情况是( )
在双缝干涉实验中,双缝到光屏上P点的距离之差0.6μm,若分别用频率为f1=5.0×1014Hz和f2=7.5×1014Hz的单色光垂直照射双缝,则 P点出现明、暗条纹的情况是( )| A. | 单色光f1和f2分别照射时,均出现明条纹 | |
| B. | 单色光f1和f2分别照射时,均出现暗条纹 | |
| C. | 单色光f1照射时出现明条纹,单色光f2照射时出现暗条纹 | |
| D. | 单色光f1照射时出现暗条纹,单色光f2照射时出现明条纹 |
3.对做匀变速直线运动的物体,下列说法正确的是( )
| A. | 在1s内、2s内、3s内物体通过的位移之比是1:3:5 | |
| B. | 一质点的位置坐标函数是x=4t+2t2,则它运动的初速度是4m/s,加速度是2m/s2 | |
| C. | 做匀减速直线运动的物体,位移一定随时间均匀减小 | |
| D. | 任意两个连续相等时间间隔内物体的位移之差都相等 |
20.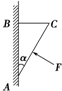 如图所示,质量为m、横截面为直角三角形的物块ABC,∠BAC=α,AB边靠在竖直墙面上,F是垂直于斜面AC的推力.物块与墙面间的动摩擦因数为μ(μ<1).现物块静止不动,则( )
如图所示,质量为m、横截面为直角三角形的物块ABC,∠BAC=α,AB边靠在竖直墙面上,F是垂直于斜面AC的推力.物块与墙面间的动摩擦因数为μ(μ<1).现物块静止不动,则( )
 如图所示,质量为m、横截面为直角三角形的物块ABC,∠BAC=α,AB边靠在竖直墙面上,F是垂直于斜面AC的推力.物块与墙面间的动摩擦因数为μ(μ<1).现物块静止不动,则( )
如图所示,质量为m、横截面为直角三角形的物块ABC,∠BAC=α,AB边靠在竖直墙面上,F是垂直于斜面AC的推力.物块与墙面间的动摩擦因数为μ(μ<1).现物块静止不动,则( )| A. | 物块可能受到4个力作用 | |
| B. | 物块受到墙的摩擦力的方向一定向上 | |
| C. | 物块对墙的压力一定为Fcos α | |
| D. | 物块受到摩擦力的大小可能等于F |
7.原子核发生β衰变时,此β粒子是( )
| A. | 原子核外的最外层电子 | |
| B. | 原子核外的电子跃迁时放出的光子 | |
| C. | 原子核内存在着电子 | |
| D. | 原子核内的一个中子变成一个质子时,放射出一个电子 |
5. 在轧制钢板时需要动态地监测钢板厚度,其检测装置由放射源、探测器等构成,如图所示.该装置中探测器接收到的是( )
在轧制钢板时需要动态地监测钢板厚度,其检测装置由放射源、探测器等构成,如图所示.该装置中探测器接收到的是( )
 在轧制钢板时需要动态地监测钢板厚度,其检测装置由放射源、探测器等构成,如图所示.该装置中探测器接收到的是( )
在轧制钢板时需要动态地监测钢板厚度,其检测装置由放射源、探测器等构成,如图所示.该装置中探测器接收到的是( )| A. | β射线 | B. | α射线 | C. | x射线 | D. | γ射线 |
 在做测定玻璃折射率的实验时,某同学为了避免笔尖接触光学面,画出的a′b′和c′d′都比实际侧面向外侧平移了一些,如图所示,以后的操作均正确,画光路图时将入射点和折射点都确定在a′b′和c′d′上,则测出的n值将偏小.
在做测定玻璃折射率的实验时,某同学为了避免笔尖接触光学面,画出的a′b′和c′d′都比实际侧面向外侧平移了一些,如图所示,以后的操作均正确,画光路图时将入射点和折射点都确定在a′b′和c′d′上,则测出的n值将偏小.
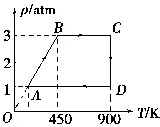 如图所示,一定质量的某种气体从状态A经B、C、D再回到A,已知气体在状态A时体积为1L,则其在状态C体积2L.
如图所示,一定质量的某种气体从状态A经B、C、D再回到A,已知气体在状态A时体积为1L,则其在状态C体积2L.