题目内容
9. 如图(a)所示,两根足够长的平行光滑导轨MN、PQ相距为L,导轨平面与水平面的夹角为α,导轨电阻不计,整个导轨放在垂直导轨平面向上的匀强磁场中.长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m.两金属导轨的上端与右端的电路连接,R是阻值可调的电阻箱,其最大值远大于金属棒的电阻值.将金属棒由静止释放,当R取不同的值时,金属棒沿导轨下滑会达到不同的最大速度vm,其对应的关系图象如图(b)所示,图中v0、R0为已知,重力加速度取g.请完成下列问题:
如图(a)所示,两根足够长的平行光滑导轨MN、PQ相距为L,导轨平面与水平面的夹角为α,导轨电阻不计,整个导轨放在垂直导轨平面向上的匀强磁场中.长为L的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m.两金属导轨的上端与右端的电路连接,R是阻值可调的电阻箱,其最大值远大于金属棒的电阻值.将金属棒由静止释放,当R取不同的值时,金属棒沿导轨下滑会达到不同的最大速度vm,其对应的关系图象如图(b)所示,图中v0、R0为已知,重力加速度取g.请完成下列问题:(1)匀强磁场的磁感应强度为多少?
(2)金属棒的电阻值为多少?
(3)当R=R0时,由静止释放金属棒,在金属棒加速运动的整个过程中,通过R的电量为q,求在这个过程中R上产生的热量为多少?
(4)R取不同值时,R的电功率的最大值不同.有同学认为,当R=R0时R的功率会达到最大.如果你认为这种说法是正确的,请予以证明,并求出R的最大功率;如果你认为这种说法是错误的,请通过定量计算说明理由.
分析 (1)金属棒下滑达到最大速度时做匀速运动,由平衡条件和安培力求得B.
(2)图象横轴截距大小等于R0.
(3)由q=△ΦR+r△ΦR+r求出金属棒下滑的距离S,根据能量守恒定律求出热量.
(4)推导功率的表达式判断正误
解答 解:(1)安培力:FA=BIL=B2L2vmRab+RB2L2vmRab+R,
金属棒匀速运动时速度最大,金属棒匀速运动,处于平衡状态,
由平衡条件得:mgsinα=B2L2vmRab+RB2L2vmRab+R,解得:vm=mgsinα(Rab+R)B2L2,
由图线斜率:k=v0R0=mgsinαB2L2,解得:B=√mgR0sinαL2v0;
(2)由图线在横轴上的截距可得:Rab=R0;
(3)当R=R0时,vm=2v0,
电荷量:q=I△t=△Φ△t(R+R0)•△t=△Φ2R0=BLs2R0,解得:s=2qR0BL,
由能量守恒定律可知,热量:
Q=12(mgsinαs-12mvm2)=12mgsinα2qR0BL-mv02=q√mgsinαR0v0-mv02;
(4)这种说法错误.
R的最大值电功率:P=I2R=m2g2sin2αB2L2R,
m2g2sin2αB2L2是恒量,则:P∝R,
P随R增大而增大,无最大值.
答:(1)匀强磁场的磁感应强度为√mgR0sinαL2v0;
(2)金属棒的电阻值为R0;
(3)在这个过程中R上产生的热量为:q√mgsinαR0v0-mv02;
(4)说法错误,无最大功功率.
点评 本题是电磁感应与力学的综合题,常常用到两个经验公式:安培力F安=B2L2vR+r和感应电量q=n△ΦR+r.

练习册系列答案
相关题目
10.平行板电容器充电后,两极板与电源断开,当用有绝缘的手柄,设法把电容器两极板距离拉大些时,下列结论正确的是( )
| A. | 电容器极板的带电量Q变大 | B. | 电容器两极板间的场强E增加 | ||
| C. | 电容器两极板间的电势差U增加 | D. | 电容器的电容C增加 |
8.某物体运动的位移-时间图象如图所示,下列说法正确的是( )
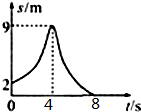

| A. | 物体做直线运动 | B. | 物体运动轨迹是曲线 | ||
| C. | 在t=4s时物体速度最大 | D. | t=8s时物体离开出发点最远 |
4.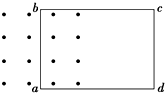 闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
 闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )
闭合线圈abcd运动到如图所示的位置时,bc边所受到的磁场力的方向向下,那么线圈的运动情况是( )| A. | 向左平动进入磁场 | B. | 向右平动进入磁场 | ||
| C. | 向上平动 | D. | 向下平动 |
14. 2013年7月,我国东北三省遭受特大暴雨袭击,给老百姓的生命安全带来巨大危害,也使人们的财产受到了严重损失.如图是某一救人的场面,为了营救一被困人员到一条河流的对岸,将一根绳的两端分别拴在两岸上的建筑物上,这根绳称为主绳,主绳上挂一个挂钩,其下连着一人,人的腰处还连着两根辅助的绳子,用来调整人的速度及位置.在此人沿着主绳离开建筑物移向对岸的过程中,假设挂钩与主绳间无摩擦,此人移动缓慢,且两根辅助绳子处于松弛状态,下列说法中正确的是( )
2013年7月,我国东北三省遭受特大暴雨袭击,给老百姓的生命安全带来巨大危害,也使人们的财产受到了严重损失.如图是某一救人的场面,为了营救一被困人员到一条河流的对岸,将一根绳的两端分别拴在两岸上的建筑物上,这根绳称为主绳,主绳上挂一个挂钩,其下连着一人,人的腰处还连着两根辅助的绳子,用来调整人的速度及位置.在此人沿着主绳离开建筑物移向对岸的过程中,假设挂钩与主绳间无摩擦,此人移动缓慢,且两根辅助绳子处于松弛状态,下列说法中正确的是( )
 2013年7月,我国东北三省遭受特大暴雨袭击,给老百姓的生命安全带来巨大危害,也使人们的财产受到了严重损失.如图是某一救人的场面,为了营救一被困人员到一条河流的对岸,将一根绳的两端分别拴在两岸上的建筑物上,这根绳称为主绳,主绳上挂一个挂钩,其下连着一人,人的腰处还连着两根辅助的绳子,用来调整人的速度及位置.在此人沿着主绳离开建筑物移向对岸的过程中,假设挂钩与主绳间无摩擦,此人移动缓慢,且两根辅助绳子处于松弛状态,下列说法中正确的是( )
2013年7月,我国东北三省遭受特大暴雨袭击,给老百姓的生命安全带来巨大危害,也使人们的财产受到了严重损失.如图是某一救人的场面,为了营救一被困人员到一条河流的对岸,将一根绳的两端分别拴在两岸上的建筑物上,这根绳称为主绳,主绳上挂一个挂钩,其下连着一人,人的腰处还连着两根辅助的绳子,用来调整人的速度及位置.在此人沿着主绳离开建筑物移向对岸的过程中,假设挂钩与主绳间无摩擦,此人移动缓慢,且两根辅助绳子处于松弛状态,下列说法中正确的是( )| A. | 主绳中的拉力先变小后变大 | B. | 主绳中的拉力先变大后变小 | ||
| C. | 主绳中的拉力不变 | D. | 主绳中的拉力变化情况无法确定 |
1.分别标有“220V,40W“和“220V,60W“字样的甲、乙两盏电灯,若将它们串联起来仍接在220伏的电路中,则下列判断中正确的是( )
| A. | 甲灯亮些 | B. | 乙灯亮些 | C. | 两灯一样亮 | D. | 无法判定 |
 如图所示,是某白炽灯泡的电流I和电压U关系的图象,该灯泡的额定电压为48V,请你根据图象回答下列问题:
如图所示,是某白炽灯泡的电流I和电压U关系的图象,该灯泡的额定电压为48V,请你根据图象回答下列问题: 如图所示为一正弦交流发电机的简化图,线圈abcd的面积是0.05m2,共100匝,线圈电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=
如图所示为一正弦交流发电机的简化图,线圈abcd的面积是0.05m2,共100匝,线圈电阻为1Ω,外接电阻R=9Ω,匀强磁场的磁感应强度B=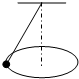 绳长一定,绳的上端固定,下端系一小球,小球在水平面 上做匀速圆周运动,如图,则小球的运动周期T、速率v、角速度ω跟绳与竖直线之间的夹角θ的关系是:θ越大,( )
绳长一定,绳的上端固定,下端系一小球,小球在水平面 上做匀速圆周运动,如图,则小球的运动周期T、速率v、角速度ω跟绳与竖直线之间的夹角θ的关系是:θ越大,( )