题目内容
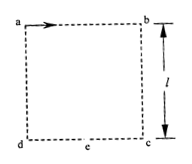
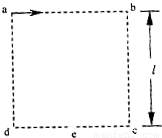
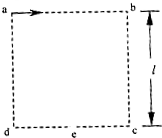 如图所示,已知正方形abcd边长为l,e是cd边的中点,abcd所围区域内是一个磁感应强度大小为B、方向垂直于纸面的匀强磁场,一带电粒子从静止开始经电压为U的电场加速后从a点沿ab方向射入磁场,最后恰好从e点射出.不计带电粒子的重力.求
如图所示,已知正方形abcd边长为l,e是cd边的中点,abcd所围区域内是一个磁感应强度大小为B、方向垂直于纸面的匀强磁场,一带电粒子从静止开始经电压为U的电场加速后从a点沿ab方向射入磁场,最后恰好从e点射出.不计带电粒子的重力.求(1)带电粒子的电量与质量的比值q/m;
(2)带电粒子从a点到e点的运动时间.
分析:(1)带电粒子先经电场加速,后进入磁场偏转.先由动能定理得到加速获得的速度表达式,在磁场中,粒子由洛伦兹力提供向心力做匀速圆周运动,画出轨迹,由几何知识求出轨迹半径,即可由牛顿第二定律求出电量与质量的比值;
(2)由几何关系得到轨迹对应的圆心角β,由圆周运动知识得到周期T,由t=
T求时间.
(2)由几何关系得到轨迹对应的圆心角β,由圆周运动知识得到周期T,由t=
| β |
| 2π |
解答: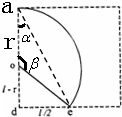 解:(1)粒子经电场加速后,由动能定理得:qU=
解:(1)粒子经电场加速后,由动能定理得:qU=
mv2
射入磁场后,有:qvB=m
粒子在磁场中的运动轨迹如图所示,几何关系是:(l-r)2+(
)2=r2
联立解得:带电粒子的电量与质量的比值为:
=
(2)由几何关系得 α=
则得粒子轨迹所对应的圆心角为 β=
由qvB=m
得r=
周期为 T=
∴T=
带电粒子从a点到e点的运动时间为 t=
T
解得:t=
T=
=
答:
(1)带电粒子的电量与质量的比值为
.
(2)带电粒子从a点到e点的运动时间为
.
 解:(1)粒子经电场加速后,由动能定理得:qU=
解:(1)粒子经电场加速后,由动能定理得:qU=| 1 |
| 2 |
射入磁场后,有:qvB=m
| v2 |
| r |
粒子在磁场中的运动轨迹如图所示,几何关系是:(l-r)2+(
| l |
| 2 |
联立解得:带电粒子的电量与质量的比值为:
| q |
| m |
| 128U |
| 25B2l2 |
(2)由几何关系得 α=
| π |
| 6 |
则得粒子轨迹所对应的圆心角为 β=
| 2π |
| 3 |
由qvB=m
| v2 |
| r |
| mv |
| qB |
周期为 T=
| 2πr |
| v |
∴T=
| 2πm |
| qB |
带电粒子从a点到e点的运动时间为 t=
| β |
| 2π |
解得:t=
| 1 |
| 3 |
| 2πm |
| 3qB |
| 50πBl2 |
| 384U |
答:
(1)带电粒子的电量与质量的比值为
| 128U |
| 25B2I2 |
(2)带电粒子从a点到e点的运动时间为
| 50πBl2 |
| 384U |
点评:本题考查粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,根据牛顿第二定律,推导出的半径与周期公式,并掌握动能定理在此应用,同时还掌握几何关系的运用.

练习册系列答案
相关题目
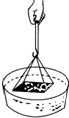 把一块干净的玻璃板吊在橡皮筋的下端,使玻璃板水平地接触水面,如图所示.已知正方形玻璃板的边长为L,水的密度为P,摩尔质量为M,阿伏加德罗常数为NA.如果把水分子看成是正方体的,试估算与玻璃板接触的水分子数为.
把一块干净的玻璃板吊在橡皮筋的下端,使玻璃板水平地接触水面,如图所示.已知正方形玻璃板的边长为L,水的密度为P,摩尔质量为M,阿伏加德罗常数为NA.如果把水分子看成是正方体的,试估算与玻璃板接触的水分子数为.