题目内容
1.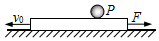 如图所示,质量M=10kg的长方体木箱,长L=1.5m,高h=0.8m,在水平面上向左做直线运动.当木箱的速度v0=3.6m/s时,对木箱施加一个方向水平向右的恒力F=50N,并同时将质量m=l kg的小球轻放在距木箱右端$\frac{L}{3}$的P点(小球可视为质点,放在P点时相对于地面的速度为零),经过一段时间,小球脱离木箱落到地面.已知木箱上表面光滑,其与地面的动摩擦因数μ=0.2.取g=10m/s2.试求:
如图所示,质量M=10kg的长方体木箱,长L=1.5m,高h=0.8m,在水平面上向左做直线运动.当木箱的速度v0=3.6m/s时,对木箱施加一个方向水平向右的恒力F=50N,并同时将质量m=l kg的小球轻放在距木箱右端$\frac{L}{3}$的P点(小球可视为质点,放在P点时相对于地面的速度为零),经过一段时间,小球脱离木箱落到地面.已知木箱上表面光滑,其与地面的动摩擦因数μ=0.2.取g=10m/s2.试求:(1)小球脱离木箱前,木箱的加速度;
(2)小球放到P点后,木箱向左运动的最大位移;
(3)小球落到地面时,木箱的速度.
分析 (1)对木箱受力分析,运用牛顿第二定律即可求出木箱的加速度;
(2)先求出小球离开木箱时木箱的位移,再根据牛顿第二定律求出小球从木箱上掉下后木箱的加速度,根据速度位移公式求出木箱的位移,两个过程的总位移即木箱向左运动的最大位移;
(3)在小球自由下落到地面的时间内,木箱先向左减速到0,后反向加速,结合牛顿第二定律和速度时间关系式即可求解小球落到地面时,木箱的速度;
解答 解:(1)小球放到木箱上后相对地面静止,
木箱的加速度大小:${a}_{1}^{\;}=\frac{F+μ(M+m)g}{M}$=$\frac{50+0.2×11×10}{10}=7.2m/{s}_{\;}^{2}$
方向:水平向左
(2)当小球离开木箱时,木箱的位移:${x}_{1}^{\;}=0.5m$
木箱的速度大小:${v}_{1}^{\;}=\sqrt{{v}_{0}^{2}-2a{x}_{1}^{\;}}=\sqrt{3.{6}_{\;}^{2}-2×7.2×0.5}$=2.4m/s
小球从木箱上掉下后,木箱的加速度大小:
${a}_{2}^{\;}=\frac{F+μMg}{M}$=$\frac{50+0.2×10×10}{10}$=$7.0m/{s}_{\;}^{2}$
木箱向左继续运动的位移:${x}_{2}^{\;}=\frac{0-{v}_{1}^{2}}{2{a}_{2}^{\;}}=\frac{0-2.{4}_{\;}^{2}}{2×(-7)}m=0.41m$
小球放到P点后,木箱向左的最大位移:${x}_{m}^{\;}={x}_{1}^{\;}+{x}_{2}^{\;}=0.5+0.41=0.91m$
(3)小球从木箱上掉下后,木箱向左的时间:${t}_{1}^{\;}=\frac{0-{v}_{1}^{\;}}{-{a}_{2}^{\;}}=\frac{0-2.4}{-7.0}=\frac{2.4}{7}s$
小球自由下落时间:${t}_{Ⅰ}^{\;}=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×0.8}{10}}s=0.4s$$>{t}_{1}^{\;}$
所以,木箱已经返回向右运动
返回时间:${t}_{2}^{\;}={t}_{Ⅰ}^{\;}-{t}_{1}^{\;}=0.4-\frac{2.4}{7}=\frac{0.4}{7}s$
返回的加速度:${a}_{3}^{\;}=\frac{F-μMg}{M}=\frac{50-20}{10}m/{s}_{\;}^{2}=3.0m/{s}_{\;}^{2}$
小球落地时,木箱的速度大小:${v}_{2}^{\;}={a}_{3}^{\;}{t}_{2}^{\;}=3.0×\frac{0.4}{7}=0.17m/s$
方向:水平向右
答:(1)小球脱离木箱前,木箱的加速度$7.2m/{s}_{\;}^{2}$,方向水平向左;
(2)小球放到P点后,木箱向左运动的最大位移为0.91m;
(3)小球落到地面时,木箱的速度为0.17m/s,方向水平向右
点评 本题采用牛顿运动定律和运动学公式结合的方法求解,也可以根据动能定理求解木箱向左运动的最大距离.

| A. | 电阻R=$\frac{U}{I}$ | B. | 电流强度I=$\frac{U}{R}$ | C. | 电场强度E=$\frac{F}{q}$ | D. | 电容C=$\frac{Q}{U}$ |
 如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )
如图是我国于2016年10月19日发射的神州十一号飞船.神州十一号和天宫二号都绕地运行,神州十一号跑“内圈”追赶天宫二号,经过五次变轨,螺旋线递进,步步靠近,在距地面高393km处完成了“天神之吻”,成功对接.则( )| A. | 神州十一号需要通过加速才能向“外圈”变轨 | |
| B. | 神州十一号在变轨追赶天宫二号的过程中机械能守恒 | |
| C. | 神州十一号与天宫二号对接时绕地运行的速度为零 | |
| D. | 神州十一号在“内圈”绕地运行的速度小于天宫二号绕地运行的速度 |
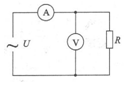 在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )
在如图所示电路中,已知交流电源电压U=311sin(100πt)V,电阻R=100欧.则电流表和电压表的读数分别为( )| A. | 3.11A,311V | B. | 2.2A,220V | C. | 2.2A,311V | D. | 3.11A,220V |
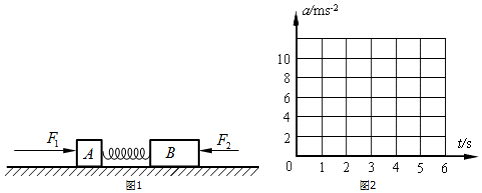
 如图所示,光滑水平面上放置质量分别为m、2m和3m的三个木块,其中质量为m的木块放在质量为2m的木块上,质量为2m和3m的木块间用一不可伸长的轻绳相连,轻绳能承受的最大拉力为FT.现用水平拉力F拉质量为3m的木块,使三个木块以同一加速度运动,下列说法正确的是( )
如图所示,光滑水平面上放置质量分别为m、2m和3m的三个木块,其中质量为m的木块放在质量为2m的木块上,质量为2m和3m的木块间用一不可伸长的轻绳相连,轻绳能承受的最大拉力为FT.现用水平拉力F拉质量为3m的木块,使三个木块以同一加速度运动,下列说法正确的是( )| A. | 质量为2 m的木块受到四个力的作用 | |
| B. | 当F逐渐增大到FT时,轻绳刚好被拉断 | |
| C. | 当F逐渐增大到1.5FT时,轻绳还不会被拉断 | |
| D. | 轻绳刚要被拉断时,质量为m和2 m的木块间的摩擦力为$\frac{{F}_{T}}{3}$ |

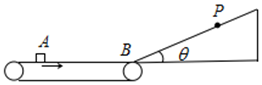 如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求:
如图所示,足够长的浅色传送带以速度v0=8m/s顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量m=1kg的墨色小滑块从距离B点s0=10m的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为μ1=0.4,斜面倾角θ=37°,斜面足够长,滑块与斜面的动摩擦因数μ2=0.45,重力加速度g=10m/s2,sin37°=0.6cos37°=0.8,求: