题目内容
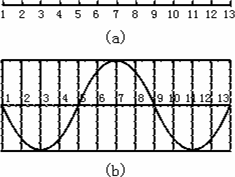
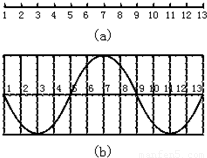
 在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图(a)所示,振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成的波形图如图(b)所示,则该波的周期T,波速v分别是( )
在均匀的介质中,各质点的平衡位置在同一直线上,相邻两个质点的距离均为a,如图(a)所示,振动从质点1开始并向右传播,其振动初速度方向竖直向上,经过时间t,前13个质点第一次形成的波形图如图(b)所示,则该波的周期T,波速v分别是( )分析:本题应根据波传播的周期性和振动传播的特点,画出波的图象(振动应传播到第17个质点),或从第13个质点此时的振动方向向下数到再经
T振动方向才向上,从而找出周期T与时间t的关系,然后求解即可.
| 1 |
| 2 |
解答:解:根据振动的周期性和波的传播特点可知,质点13此时的振动方向向下,而波源的起振方向向上,所以从质点13算起,需要再经
T振动的方向才能向上,即与波源的起振方向相同,设周期为T,则t=
T+
T=2T,即T=
.
由题意知,λ=8a,结合λ=vT,T=
,可得v=
.
故选A
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
由题意知,λ=8a,结合λ=vT,T=
| t |
| 2 |
| 16a |
| t |
故选A
点评:“经过时间t,前13个质点第一次形成如图10-9-20乙所示的波形”,并不说波只传到前13个质点.如果是只传到前13个质点,由于第13个质点此时振动方向向下,所以质点1开始运动时的速度方向也应该竖直向下,这与题给条件矛盾,熟记:任何质点的起振方向均与波源的起振方向相同.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

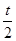 ,v=
,v=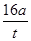 B.T=
B.T=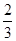 t,v=
t,v=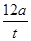
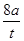 D.T=
D.T=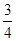 t,v=
t,v=
 ,v=
,v=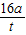
 t,v=
t,v=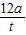
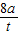
 t,v=
t,v=