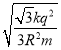��Ŀ����
����Ŀ����ͼ��ʾΪһ������Ϸװ�ã�����L1=1m��ˮƽ���AB���Ҷ˹̶��������������B����뾶Ϊr=0.2m�İ�Բ�ι⻬��ֱ���ƽ�����ӣ����Բ�ι��Բ��O��ȸߴ��̶�һ����L2=0.2m��ˮƽ��DE��ˮƽ�����D���O�����L3=0.2m����֪��������m=0.5kg������Ϊ�ʵ㣬��ʼʱ�����ڵ���ԭ����A�㣬�����뵯��δ˩�ӣ�����ʱ�Ӿ�ֹ�ͷŻ����ҵ��ɵĵ���������ȫת��Ϊ���鶯�ܣ�������AB��Ķ�Ħ��������=0.5�����Կ���������ÿ����Ϸ��Ҫ���ܰ�ȫͨ����Բ�ι����ߵ�C����
��1��������ǡ����ͨ��Բ�ι����ߵ�Cʱ���ٶȴ�СvC��
��2�������鵽��B��ʱ���ٶ�ΪvB=4m/s��������B��ʱ��Բ�ι����ѹ��FN��С�����ɵ�������Ep0��
��3����Ҫ������������ˮƽ��DE�������������ķ����������Ӧ���ɵ������ܵ�ȡֵ��Χ��
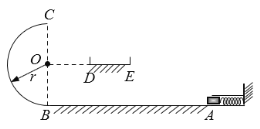
���𰸡���1��![]() ����2��45N��6.5J����3��
����2��45N��6.5J����3��![]()
��������
��1�����ڻ���ǡ����ͨ��Բ�ι����ߵ�C���ɵ�
![]()
�������ݽ��
![]()
��2����B�㣬��ţ�ٵڶ����ɵ�
![]()
�������ݽ��
![]()
����ţ�ٵ������ɣ������Բ�����ѹ����СΪ45N
����ʱ�Ӿ�ֹ�ͷŵ������˶���B�Ĺ����У����ݶ��ܶ�����
![]()
�������ݽ��
![]()
��3�������C��ɳ�����ƽ���˶����ɵ�
![]()
���
![]()
ˮƽ������
![]()
����Ҫ��Ҫ������ˮƽ��DE����x1=0.2m��x2=0.4m �������ݽ��
![]() ��
��![]()
����ΪҪ��ȫͨ��C�㣬����
![]()
����ʱ�Ӿ�ֹ�ͷŵ������˶���C�Ĺ����У����ݶ��ܶ�����
![]()
���
![]()
���ɵ������ܵ�ȡֵ��ΧΪ
![]()