Question

【题目】如图,在0≤x≤d的空间,存在垂直xOy平面的匀强磁场,方向垂直xOy平面向里。y轴上P点有一小孔,可以向y轴右侧垂直于磁场方向不断发射速率均为v、与y轴所成夹角θ可在0～180°范围内变化的带负电的粒子。已知θ=45°时,粒子恰好从磁场右边界与P点等高的Q点射出磁场,不计重力及粒子间的相互作用。求：

(1)磁场的磁感应强度。

(2)若θ=30°,粒子射出磁场时与磁场边界的夹角(可用三角函数、根式表示)。

Answer 1

【答案】（1）略（2） 略

【解析】（1）当θ=45°时，粒子恰好从磁场右边界与P点等高的Q点射出磁场，
由几何关系可得，d=2Rcos45°
解得：R＝d
粒子仅在洛伦兹力作用下，则有：
所以，
（2）根据半径的大小R＝ d与入射角30°，可画出右图，

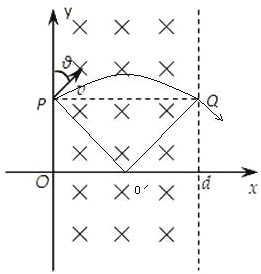
△PO′Q中，∠PO′Q=60°，PO′=R， ，
则三角形正弦定理可得， ，
设粒子射出磁场时与磁场边界的夹角为β，则有cosβ＝sinα＝
所以θ＝arccos()