Question

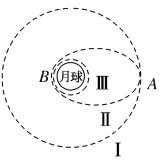
【题目】如图所示，设月球半径为R，假设“嫦娥四号”探测器在距月球表面高度为3R的圆形轨道Ⅰ上做匀速圆周运动，运行周期为T，到达轨道的A点时点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B时，再次点火进入近月轨道Ⅲ绕月做匀速圆周运动，引力常量为G，不考虑其他星球的影响，则下列说法正确的是(　　)

A.月球的质量可表示为

B.在轨道Ⅲ上B点的速率大于在轨道Ⅱ上B点的速率

C.“嫦娥四号”探测器沿椭圆轨道从A点向B点运动过程中，机械能保持不变

D.“嫦娥四号”探测器从远月点A向近月点B运动的过程中，加速度变小

Answer 1

【答案】AC

【解析】

A．在轨道Ⅰ上运动过程中，万有引力充当向心力，故有

G＝m·4R

解得

M＝

故A正确；

B．在轨道Ⅱ的B点需要减速做近心运动才能进入轨道Ⅲ做圆周运动，所以在轨道Ⅲ上B点速率小于在轨道Ⅱ上B点的速率，故B错误；

C．探测器沿椭圆轨道从A运动到B的过程中只受到月球引力作用，探测器的机械能保持不变，故C正确；

D．根据公式

G＝ma

可得

a＝

所以距离月球越远，向心加速度越小，故从远月点到近月点运动过程中，加速度变大，故D错误。

故选AC。