Question

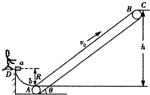如图所示，在大型超市的仓库中，要利用皮带运输机将货物由平台D运送到高为h=2.5m的平台C上．为了便于运输，仓储员在平台D与皮带间放了一个

1

4

圆周的光滑轨道ab，轨道半径为R=0.8m，轨道最低点与皮带接触良好．已知皮带和水平面间的夹角为θ=37°，皮带和货物间的动摩擦因数为μ=0.75，运输机的皮带以v₀=1m/s的速度顺时针匀速运动（皮带和轮子之间不打滑）．现仓储员将质量m=200kg货物放于轨道的a端（g=10m/s²）．求：
（1）货物到达圆轨道最低点b时对轨道的压力．
（2）货物沿皮带向上滑行多远才能相对皮带静止．
（3）皮带将货物由A运送到B需对货物做多少功．

Answer 1

分析：（1）货物由a从b过程，机械能守恒，求解出b点速度；在b点，重力和支持力的合力提供向心力，根据牛顿第二定律列式求解支持力，最后根据牛顿第三定律求解压力；
（2）对上滑过程运用动能定理列式求解即可；
（3）由于μ=tanθ=0.75，物体加速上滑达到最大速度后，与传送带一起匀速上升，静摩擦力达到最大值，等于滑动摩擦力，故摩擦力大小不变，方向反向；分减速和匀速过程运用动能定理列式求解．

解答：解：（1）货物由a到b过程，机械能守恒，有：mgR=

1

2

mv2；
解得：v=

2gR

=

2×10×0.8

=4m/s；
在b点，重力和支持力的合力提供向心力，根据牛顿第二定律，有：F-mg=m

v2

R

；
解得：F=m（g+

v2

R

）=200×（10+

42

0.8

）=6000N；
故压力为6000N；
（2）货物减速上滑过程，根据动能定理，有：(-μmgcos37°-mgsin37°)x=

1

2

m

v

2 0

-0
解得：x=0.625m；
（3）由于μ=tanθ=0.75，物体加速上滑达到最大速度后，与传送带一起匀速上升，静摩擦力达到最大值，等于滑动摩擦力，故摩擦力大小不变，方向反向；
货物匀速上升过程的上升高度为：h₁=h-xsin37°=2.5-0.625×0.6=2.215m
在x位移内皮带对货物做功为：W₁=-μmgxsin37°=-750J
在匀速上升阶段，由功能关系，得到：W₂=mgh₁=4250J
故皮带对物体做的总功为：W=W₁+W₂=-750+4250=3500J
答：（1）货物到达圆轨道最低点b时对轨道的压力为6000N．
（2）货物沿皮带向上滑行0.625m才能相对皮带静止．
（3）皮带将货物由A运送到B需对货物做3500J的功．

点评：本题关键明确滑块的运动规律，然后分阶段运用机械能守恒定律、动能定理、功能关系等列式求解，较难．