题目内容
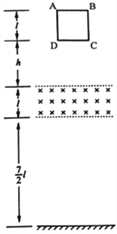
【题目】如图,匀强磁场的磁感应强度方向垂直于纸面向里,宽度为![]() ,上、下边界与地面平行,下边界与地面相距
,上、下边界与地面平行,下边界与地面相距![]() .将一个边长为
.将一个边长为![]() ,质量为m,总电阻为R的正方形刚性导电线框ABCD置于匀强磁场区域上方,线框CD边与磁场上边界平行,从高于磁场上边界h的位置静止释放,h的值能保证AB边匀速通过磁场区域.从AB边离开磁场到CD边落在地面所用时间是AB边界通过磁场时间的2倍(重力加速度为g),求:
,质量为m,总电阻为R的正方形刚性导电线框ABCD置于匀强磁场区域上方,线框CD边与磁场上边界平行,从高于磁场上边界h的位置静止释放,h的值能保证AB边匀速通过磁场区域.从AB边离开磁场到CD边落在地面所用时间是AB边界通过磁场时间的2倍(重力加速度为g),求:
(1)线框通过磁场过程中电流的方向;
(2)磁场区域磁感应强度的大小;
(3)根据CD边刚进入磁场时线框加速度a与h的函数关系,分析h在不同情况下加速度的大小和方向,计算线框通过磁场区域产生的热量。
【答案】(1)cd边在磁场中时电流方向为DCBAD,AB边在磁场中时电流方向为ABCDA;(2) ;(3)mgh.
;(3)mgh.
【解析】(1)根据楞次定律,线框中电流方向:cd边在磁场中时为DCBAD,AB边在磁场中为ABCDA;
(2)设线框AB边在磁场中做匀速运动的速度大小为v1,穿过磁场的时间为t,AB边切割磁场产生的电动势为E,线框中电流为I,则:
mg=IlB ①
E=lv1B ②
I= ![]() ③
③
由①②③解得:B= 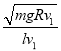 ④
④
l=v1t ⑤
依据题意和匀变速直线运动的规律,得:
![]() ⑥
⑥
由⑤⑥解得: ![]() ⑦
⑦
由④⑦解得:  ⑧
⑧
(3)设线框CD边刚进入磁场时,速度大小为v,加速度大小为a,线框产生的电动势为E,电流为I,线框通过磁场区域产生的热量为Q;
由动能定理得:mgh= ![]() -0,
-0,
解得:v= ![]() ;
;
根据切割公式和欧姆定律,有:I= ![]() ⑨
⑨
由牛顿第二定律得:mg﹣IlB=ma ⑩
由⑨⑩解得:a=(1﹣![]() )g;
)g;
当h=2l时,a=0
当h>2l时,加速度大小为(![]() ﹣1)g,方向竖直向上;
﹣1)g,方向竖直向上;
当h<2l时,加速度大小为(1﹣![]() )g,方向竖直向下;
)g,方向竖直向下;
根据能量守恒定律,有:Q=mg(h+2l)﹣![]() ⑾
⑾
由⑦⑾解得:Q=mgh;