题目内容
【题目】（选修3－4）
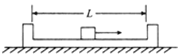
（1）一列简谐横波沿x轴正方向传播，频率为5Hz，某时刻的波形如图所示，介质中质点A在距原点8cm处，质点B在距原点16cm处，从图象对应时刻算起，质点A的运动状态与图示时刻质点B的运动状态相同所需的最短时间为
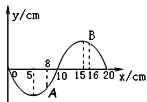
A．0.08s B．0.12s C．0.14s D．0.16s
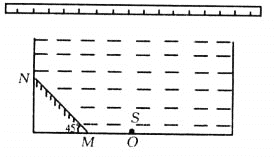
（2）如图所示，一不透明的圆柱形容器内装满折射率n＝
的透明液体，容器底部正中央O点处有一点光源S，平面镜MN与底面成45°角放置，若容器高为2dm，底边半径为（1+
）dm，OM＝1dm，在O点正上方离容器底部3dm处水平放置一足够长的刻度尺，求光源 S发出的光线经平面镜反射后，照射到刻度尺的长度（不考虑容器侧壁和液面的反射）。
【答案】（1）A （2）（1+
)dm
【解析】(1) 从波形图得到波长为λ=20cm=0.2m，波的频率为f=5Hz，故波速为v=λf=0.2×5=1m/s；
当质点B的位移和速度与图示时刻质点A的状态相同时，所需的最短时间即为波形向右平移△x=（16-8）cm=8cm=0.08m的时间，为：
，故A正确；
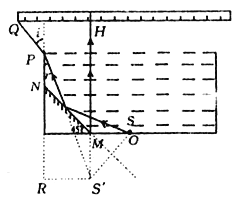
(2)作图找出发光点S在平面镜中的像点S＇，连接S＇M延长交直尺于H点，MH沿竖直方向，连接S＇P，在RtΔPR S＇中，RS＇＝dm，PR=3 dm r＝30° 由折射定律可得：
解得i＝45° 刻度尺上被照亮的范围QH＝(1+)dm
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
