题目内容
(2013?天河区一模)如图a,间距为d的平行金属板MN与一对光滑的平行导轨相连,平行导轨间距L=
,一根导体棒ab以一定的初速度向右匀速运动,棒的右端存在一个垂直纸面向里,磁感应强度大小为B的匀强磁场.棒进入磁场的同时,粒子源P释放一个初速度为零的带电粒子,已知带电粒子质量为m,电荷量为q,粒子能从N板加速到M板,并从M板上的一个小孔穿出.在板的上方,有一个环形区域内存在磁感应强度大小也为B,垂直纸面向外的匀强磁场.已知外圆半径为2d,内圆半径为d,两圆的圆心与小孔重合(粒子重力不计).
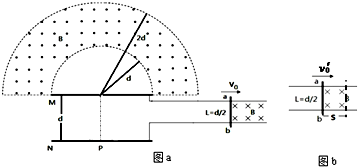
(1)判断带电粒子的正负,并求当ab棒的速度为v0时,粒子到达M板的速度v;
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是多少?
(3)若棒ab的速度
=
,为使粒子不从外圆飞出,可通过控制导轨区域磁场的宽度S(如图b),则该磁场宽度S应控制在多少范围内?
| d |
| 2 |

(1)判断带电粒子的正负,并求当ab棒的速度为v0时,粒子到达M板的速度v;
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是多少?
(3)若棒ab的速度
| v | ′ 0 |
| qBd |
| m |
分析:(1)由右手定则判断ab棒产生的感应电动势方向,分析M、N两板的电性,即可判断带电粒子的电性;由公式E=BLv求出棒ab产生的感应电动势,MN板间电压就等于此感应电动势,根据动能定理求粒子到达M板的速度v;
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切,由几何关系求出轨迹半径的最大半径,由洛伦兹力充当向心力,列式求出速度的最大值,即可得到速度的范围;
(3)若棒ab的速度
=
,粒子在磁场中轨迹半径等于d,如果让粒子在MN间一直加速,则必然会从外圆飞出,所以只能让粒子在MN间只加速至最大速度(上题的结果).研究粒子在电场加速过程,由牛顿第二定律和运动学公式求出加速的时间,即可求出导轨区域磁场的宽度S.
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切,由几何关系求出轨迹半径的最大半径,由洛伦兹力充当向心力,列式求出速度的最大值,即可得到速度的范围;
(3)若棒ab的速度
| v | ′ 0 |
| qBd |
| m |
解答: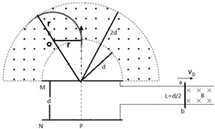 解:(1)根据右手定则知,a端为正极,故带电粒子必须带负电
解:(1)根据右手定则知,a端为正极,故带电粒子必须带负电
ab棒切割磁感线,产生的电动势U=B
v0
对于粒子,由动能定理qU=
mv2-0
得粒子射出电容器的速度为 v=
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切,
由几何关系有:(2d-r)2=r2+d2
得 r=
d
由洛仑兹力等于向心力,有:qv0B=m
联立得 v0=
故ab棒的速度范围:v0≤
(3)因为
=
>vm,故如果让粒子在MN间一直加速,则必然会从外圆飞出,
所以只能让粒子在MN间只加速至速度为 v=
=
,再匀速射出电容器则可.
而带电粒子在电场中加速过程,有
a=
=
将
=
代入得:a=
由v=
=at=
t
得:t=
对于棒ab:s=v0′t=
d
故磁场的宽度应:s≤
d
答:
(1)带电粒子带负电,当ab棒的速度为v0时,粒子到达M板的速度v是
;
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是:v0≤
.
(3)若棒ab的速度
=
,为使粒子不从外圆飞出,可通过控制导轨区域磁场的宽度S(如图b),则该磁场宽度S应控制在
d之内.
 解:(1)根据右手定则知,a端为正极,故带电粒子必须带负电
解:(1)根据右手定则知,a端为正极,故带电粒子必须带负电ab棒切割磁感线,产生的电动势U=B
| d |
| 2 |
对于粒子,由动能定理qU=
| 1 |
| 2 |
得粒子射出电容器的速度为 v=
|
(2)要使粒子不从外边界飞出,则粒子最大半径时的轨迹与外圆相切,
由几何关系有:(2d-r)2=r2+d2
得 r=
| 3 |
| 4 |
由洛仑兹力等于向心力,有:qv0B=m
| ||
| r |
联立得 v0=
| 3qBd |
| 4m |
故ab棒的速度范围:v0≤
| 3qBd |
| 4m |
(3)因为
| v | ′ 0 |
| qBd |
| m |
所以只能让粒子在MN间只加速至速度为 v=
|
| 3qBd |
| 4m |
而带电粒子在电场中加速过程,有
a=
| qU |
| md |
q(Bv0′
| ||
| md |
将
| v | ′ 0 |
| qBd |
| m |
| q2B2d |
| 2m2 |
由v=
| 3qBd |
| 4m |
| q2B2d |
| 2m2 |
得:t=
| 3m |
| 2qB |
对于棒ab:s=v0′t=
| 3 |
| 2 |
故磁场的宽度应:s≤
| 3 |
| 2 |
答:
(1)带电粒子带负电,当ab棒的速度为v0时,粒子到达M板的速度v是
|
(2)若要求粒子不能从外圆边界飞出,则ab棒运动速度v0的取值范围是:v0≤
| 3qBd |
| 4m |
(3)若棒ab的速度
| v | ′ 0 |
| qBd |
| m |
| 3 |
| 2 |
点评:本题是电场加速、磁场偏转和电磁感应的组合,根据动能定理求加速获得的速度,磁场中画轨迹等等都常规方法,关键要抓住各个过程之间的内在联系.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
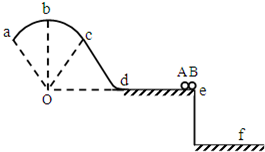 (2013?天河区一模)如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的
(2013?天河区一模)如图,竖直固定轨道abcd段光滑,长为L=1.0m的平台de段粗糙,abc段是以O为圆心的圆弧.小球A和B紧靠一起静止于e处,B的质量是A的4倍.两小球在内力作用下突然分离,A分离后向左始终沿轨道运动,与de段的动摩擦因数μ=0.2,到b点时轨道对A的支持力等于A的重力的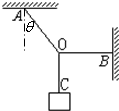 (2013?天河区一模)三段不可伸长的细绳 OA、OB、OC,悬挂一质量为m的重物,如图所示,其中OA与竖直方向的夹角为θ,OB沿水平方向,则OA、OB绳拉力大小分别为( )
(2013?天河区一模)三段不可伸长的细绳 OA、OB、OC,悬挂一质量为m的重物,如图所示,其中OA与竖直方向的夹角为θ,OB沿水平方向,则OA、OB绳拉力大小分别为( ) (2013?天河区一模)两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度-时间图象如图所示.则下列说法中正确的是( )
(2013?天河区一模)两个质点甲与乙,同时由同一地点向同一方向做直线运动,它们的速度-时间图象如图所示.则下列说法中正确的是( )