题目内容
如图所示,半径为a的圆环电阻不计,放置在垂直于纸面向里,磁感应强度为B的匀强磁场中,环内有一导体棒电阻为r,可以绕环匀速转动.将电阻R,开关S连接在环和棒的O端,将电容器极板水平放置,并联在R和开关S两端。已知两板间距为d。
(1)开关S断开,极板间有一带正电q,质量为m的微粒恰好静止,试判断OM的转动方向和角速度的大小.
(2)当S闭合时,该带电粒子以 g的加速度向下运动,则R是r的几倍?
g的加速度向下运动,则R是r的几倍?

【答案】
(1)OM应绕O点逆时针方向转动 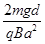 (2)3
(2)3
【解析】本题考查带电粒子在电场中的运动,导体棒切割磁感线产生的感应电动势为BRwR/2,电容器两端的电压为外电阻R两端电压,由此可求解本题
(1)由于粒子带正电,故电容器上极板为负极,根据右手定则,OM应绕O点逆时针方向转动. 2分
粒子受力平衡:mg=q  ,E=
,E= Ba2ω. 2分
Ba2ω. 2分
当S断开时,U=E,解得ω=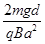 . 2分
. 2分
(2)当S闭合时,根据牛顿第二定律mg-q =m·
=m· g, 2分
g, 2分
U′=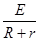 ·R,解得
·R,解得 =3. 2分
=3. 2分

练习册系列答案
相关题目
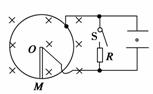

 ,求L2的功率。
,求L2的功率。
 =
= T/s,求灯L2的功率.
T/s,求灯L2的功率.